题目内容
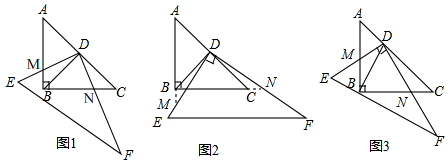
19. 如图,在矩形纸片ABCD中,AB=4,BC=5,点E在AD边上,EF⊥BC,垂足为F,点M在AB边上,BM=1,沿过点M的直线折叠该纸片,使点A落在线段EF上的点A′处,折痕为MN,点N在AD边上.
如图,在矩形纸片ABCD中,AB=4,BC=5,点E在AD边上,EF⊥BC,垂足为F,点M在AB边上,BM=1,沿过点M的直线折叠该纸片,使点A落在线段EF上的点A′处,折痕为MN,点N在AD边上.(1)画出折痕MN;(尺规作图,保留作图痕迹,不写画法)
(2)当BF=1.8时,求折痕MN的长;
(3)写出折痕MN的条数与对应的BF的长度之间的关系.
分析 (1)以M为圆心,MA长为半径画弧,交EF于A',作∠AMA'的角平分线,交AD于N,连接NA',MA',则MN是折痕;
(2)过点M作MH⊥EF于H,得出BF=MH=AE=1.8,BM=GF=1,EG=AM=3,根据勾股定理求得A'G,再设AN=x,则NE=1.8-x,NA'=x,在Rt△A'EN中,根据勾股定理得到(1.8-x)2+0.62=x2,求得AN的长,最后根据勾股定理求得MN的长即可;
(3)分情况讨论即可,当BF<2$\sqrt{2}$时,有一条折痕;当2$\sqrt{2}$≤BF<3时,有两条折痕;当BF=3时,有一条折痕;当BF>3时,无折痕.
解答 解:(1)如图所示,折痕MN即为所求;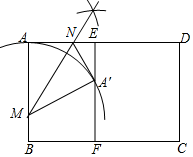
(2)过点M作MG⊥EF于G,则BF=MG=AE=1.8,BM=GF=1,EG=AM=3,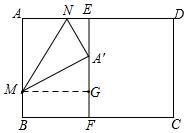
由折叠得,MA'=MA=3,
∴Rt△MA'G中,A'G=$\sqrt{{3}^{2}-1.{8}^{2}}$=2.4,
∴EA'=3-2.4=0.6,
设AN=x,则NE=1.8-x,NA'=x,
∴Rt△A'EN中,(1.8-x)2+0.62=x2,
解得x=1,
∴AN=1,
∴Rt△AMN中,MN=$\sqrt{A{M}^{2}+A{N}^{2}}$=$\sqrt{10}$;
(3)连接MF,
因为当MF=MA'=3时,Rt△BMF中,BF=$\sqrt{{3}^{2}-{1}^{1}}$=2$\sqrt{2}$,
故当BF<2$\sqrt{2}$时,有一条折痕;
因为当MA'⊥EF时,BF=MA'=3,
故当2$\sqrt{2}$≤BF<3时,有两条折痕;
当BF=3时,有一条折痕;
当BF>3时,无折痕.
点评 本题主要考查了矩形的性质以及折叠的性质,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
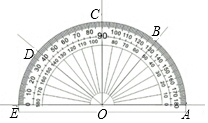 已用点A、B、C、D、E的位置如图所示,下列结论中正确的是( )
已用点A、B、C、D、E的位置如图所示,下列结论中正确的是( )| A. | ∠AOB=130° | B. | ∠AOB=∠DOE | C. | ∠DOC与∠BOE互补 | D. | ∠AOB与∠COD互余 |
(Ⅰ)根据题意,填写下表:
| 攒钱的月数/个 | 3 | 6 | … | x |
| 小明攒钱的总数/元 | 350 | 500 | … | 200+50x |
| 小强攒钱的总数/元 | 330 | 510 | … | 150+60x |
(Ⅲ)若这种火车模型的价格为780元,他们谁能够先买到该模型?
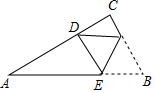 如图,Rt△ABC纸片,∠C=90°,∠A=30°,BC=3,将∠B翻折压平,并使顶点B落在AC边上点D处,则AE的取值范围是3≤AE≤4.
如图,Rt△ABC纸片,∠C=90°,∠A=30°,BC=3,将∠B翻折压平,并使顶点B落在AC边上点D处,则AE的取值范围是3≤AE≤4.