��Ŀ����
����Ŀ�������������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������C1��y1=��2x2+4x+2��C2��u2=��x2+mx+nΪ���Ѻ������ߡ���
��1����������C2�Ľ���ʽ��
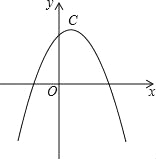
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
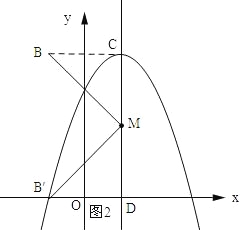
��3����������C2�Ķ���ΪC����B������Ϊ����1��4��������C2�ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������C2�ϣ������������M�����꣬������˵�����ɣ�
���𰸡���1��u2=��x2+2x+3����2��![]() ����3��M��1��2����1��5��.
����3��M��1��2����1��5��.
��������
�����������1�������C1���㣬�ٸ������������Ѻ�������������ֱ�ӵó�C2�Ķ���ʽ���ٻ���һ��ʽ���ɣ���2�����ú��������ֵ������A��a����a2+2a+3������OQ=x��AQ=��a2+2a+3���õ�OQ+AQ��a�ĺ�����ϵʽ�������ú�����ֵ���OQ+AQ����ֵ����3������BC������B����B��D��CM������ΪD������BCM�ա�MDB��������BC=MD��CM=B��D�����M������Ϊ��1��a������ʾ����B�������꣬����B����������������ߵĽ���ʽ�����a��ֵ���Ӷ��õ���M�����꣮
��������� ��1����y1=��2x2+4x+2=��2��x��1��2+4����������C1�Ķ�������Ϊ��1��4������������C1��C2������ͬ���� u2=����x��1��2+4=��x2+2x+3����������C2�Ľ���ʽΪu2=��x2+2x+3����2����ͼ1�� ���A������Ϊ��a����a2+2a+3������AQ=��a2+2a+3��OQ=a����AQ+OQ=��a2+2a+3+a=��a2+3a+3=![]() ��
��
����a=![]() ʱ��AQ+OQ�����ֵ�����ֵΪ
ʱ��AQ+OQ�����ֵ�����ֵΪ![]() ����3����ͼ2������BC������B����B��D��CM������ΪD��
����3����ͼ2������BC������B����B��D��CM������ΪD��
��B����1��4����C��1��4���������ߵĶԳ���Ϊx=1����BC��CM��BC=2���ߡ�BMB��=90�������BMC+��B��MD=90����
��B��D��MC�����MB��D+��B��MD=90�������MB��D=��BMC����BM=B��M�����BCM�ա�MDB������BC=MD��CM=B��D��
���M������Ϊ��1��a������B��D=CM=4��a��MD=CB=2������B��������Ϊ��a��3��a��2�����ੁ��a��3��2+2��a��3��+3=a��2�����a1=2��a2=5����a=2ʱ��M������Ϊ��1��2������a=5ʱ��M������Ϊ��1��5����
������������M������Ϊ��1��2����1��5��ʱ��B��ǡ������������C2�ϣ�