题目内容
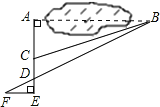
【题目】如图,E点是正方形ABCD的边BC上一点,AB=12,BE=5,△ABE逆时针旋转后能够与△ADF重合.
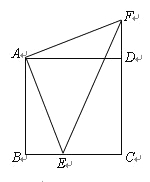
(1)旋转中心是 ,旋转角为 度;
(2)△AEF是 三角形;
(3)求EF的长.
【答案】(1)点A,90°;(2)等腰直角;(3)![]()
【解析】
(1)根据图形和已知即可得出答案.
(2)根据旋转得出全等,根据全等三角形的性质得出∠BAE=∠DAF,AE=AF,求出∠EAF=∠BAD,即可得出答案.
(3)求出AE,求出AF,根据勾股定理求出EF即可.
解:(1)从图形和已知可知:旋转中心是点A,旋转角的度数等于∠BAD的度数,是90°,
故答案为:点A,90;
(2)等腰直角三角形,
理由是:∵四边形ABCD是正方形,
∴∠BAD=90°,
∵△ABE逆时针旋转后能够与△ADF重合,
∴△ABE≌△ADF,
∴∠BAE=∠DAF,AE=AF,
∴∠FAE=∠FAD+∠DAE=∠BAE+∠DAE=∠BAD=90°,
∴△AEF是等腰直角三角形,
故答案为:等腰直角.
(3)由旋转可知∠EAF=90°,△ABE≌△ADF,
∴AE=AF,△EAF是等腰直角三角形
在Rt△ABE中,∵AB=12,BE=5
∴![]()
∴![]()

练习册系列答案
相关题目