题目内容
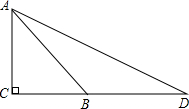
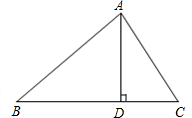
如图，在△ABC中，AD是BC上的高，tanB=cos∠DAC．
（1）求证：AC=BD；
（2）若sin∠C=
，BC=12，求AD的长．
（1）求证：AC=BD；
（2）若sin∠C=
| 12 |
| 13 |
（1）证明：∵AD是BC上的高，
∴AD⊥BC，
∴∠ADB=90°，∠ADC=90°，
在Rt△ABD和Rt△ADC中，
∵tanB=
，cos∠DAC=
，
又∵tanB=cos∠DAC，
∴
=
，
∴AC=BD．
（2）在Rt△ADC中，sinC=
，
故可设AD=12k，AC=13k，
∴CD=
=5k，
∵BC=BD+CD，又AC=BD，
∴BC=13k+5k=18k
由已知BC=12，
∴18k=12，
∴k=
，
∴AD=12k=12×
=8．
∴AD⊥BC，
∴∠ADB=90°，∠ADC=90°，
在Rt△ABD和Rt△ADC中，
∵tanB=
| AD |
| BD |
| AD |
| AC |
又∵tanB=cos∠DAC，
∴
| AD |
| BD |
| AD |
| AC |
∴AC=BD．
（2）在Rt△ADC中，sinC=
| 12 |
| 13 |
故可设AD=12k，AC=13k，
∴CD=
| AC2-AD2 |
∵BC=BD+CD，又AC=BD，
∴BC=13k+5k=18k
由已知BC=12，
∴18k=12，
∴k=
| 2 |
| 3 |
∴AD=12k=12×
| 2 |
| 3 |
练习册系列答案
相关题目
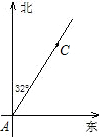航行到点B处，发现此时灯塔C与海船的距离最短；
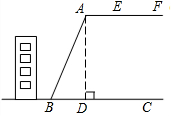，保障安全，学校决定对该土坡进行改造，经过地质人员勘测，当坡角不超过45°时，可以确保山体不滑坡．
