题目内容
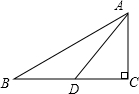
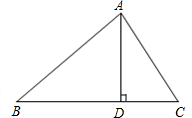
已知AD是△ABC的中线，∠ABC=30°，∠ADC=45°，则∠ACB=______度．
设AE=x，
过A作AE⊥BC，交BC延长线于E，
∵AE⊥BC，
∴∠AED=∠AEB=90°，
∵∠ADC=45°，
∴∠DAE=180°-90°-45°=45°=∠ADE，
∴AE=DE=x，
∵∠B=30°，
∴AB=2x，
由勾股定理得：BE=
x，
∴BD=DC=
x-x，
∴CE=x-（
x-x）=（2-
）x，
∵tan∠ACE=
=
=2+
，
∵tan75°=tan（45°+30°）=
=2+
∴∠ACE=75°，
则∠ACB=180°-75°=105°．
故答案为：105°．
过A作AE⊥BC，交BC延长线于E，
∵AE⊥BC，
∴∠AED=∠AEB=90°，
∵∠ADC=45°，
∴∠DAE=180°-90°-45°=45°=∠ADE，
∴AE=DE=x，
∵∠B=30°，
∴AB=2x，
由勾股定理得：BE=
| 3 |
∴BD=DC=
| 3 |
∴CE=x-（
| 3 |
| 3 |
∵tan∠ACE=
| AE |
| CE |
| x | ||
(2-
|
| 3 |
∵tan75°=tan（45°+30°）=
| tan45°-tan30° |
| 1-tan45°×tan30° |
| 3 |
∴∠ACE=75°，
则∠ACB=180°-75°=105°．
故答案为：105°．
练习册系列答案
相关题目
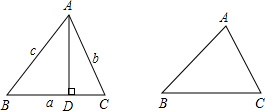
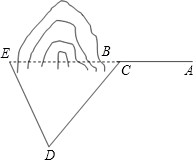需写出结论．）
