题目内容
【题目】如图,矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为( )

A. 1.5B. 3
C. 1.5或3D. 有两种情况以上
【答案】C
【解析】
分两种情况:①当∠EFC=90°时,先判断出点F在对角线AC上,利用勾股定理列式求出AC,设BE=x,表示出CE,根据翻折变换的性质可得AF=AB,EF=BE,然后在Rt△CEF中,利用勾股定理列出方程求解即可;②当∠CEF=90°时,判断出四边形ABEF是正方形,根据正方形的四条边都相等可得BE=AB.
解:分两种情况:
①当∠EFC=90°时,如图1,
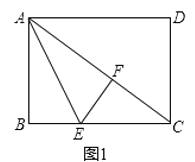
∵∠AFE=∠B=90°,∠EFC=90°,
∴点A、F、C共线,
∵矩形ABCD的边AD=4,
∴BC=AD=4,
在Rt△ABC中,![]() ,
,
设BE=x,则CE=BC﹣BE=4﹣x,
由翻折的性质得,AF=AB=3,EF=BE=x,
∴CF=AC﹣AF=5﹣3=2,
在Rt△CEF中,EF2+CF2=CE2,
即x2+22=(4﹣x)2,
解得x=1.5,
即BE=1.5;
②当∠CEF=90°时,如图2,

由翻折的性质得,∠AEB=∠AEF=![]() ×90°=45°,
×90°=45°,
∴四边形ABEF是正方形,
∴BE=AB=3,
综上所述,BE的长为1.5或3.
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目