题目内容
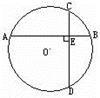
(本题满分12分)已知,AB为⊙O 的直径,点E 为弧AB 任意一点,如图,AC平分∠BAE,交⊙O于C ,过点C作CD⊥AE于D,与AB的延长线交于P.

⑴求证:PC是⊙O的切线.⑵若∠BAE=60°,求线段PB与AB的数量关系.

⑴求证:PC是⊙O的切线.⑵若∠BAE=60°,求线段PB与AB的数量关系.
略
分析:
(1)通过角平分线和有两半径为边的三角形是等腰三角形可得到OC∥AD,再证明OC⊥CD.
(2)先得到△ACB是含30°的直角三角形,找到AB=2BC,再证明BC=BP即可.
解答:
(1)证明:连OC,BC,如图,

∵∠1=∠2,
∵OA=OC,
∴∠1=∠OCA,
∴∠2=∠OCA.
∴AD∥OC.
又∵CD⊥AE,
∴OC⊥CD.
∴PC是⊙O的切线。
(2)解:若∠BAE=60°,则∠1=30°,∠P=30°。

∵AB为⊙O的直径,
∴∠BCA=90°。
∴∠3=60°,则△OBC为等边三角形,即BC=1/2AB。
而∠3=∠P+∠4,所以∠4=30°,
∴BC=BP
∴PB=1/2AB
点评:熟练掌握切线的判定定理,证明切线的问题转化为证明线段垂直的问题.要学会充分利用特殊角进行角度计算,确定边之间的数量。

练习册系列答案
相关题目
 和
和 ,两圆的圆心距是
,两圆的圆心距是 ,则两圆的位置关系是_▲_;
,则两圆的位置关系是_▲_;





 和⊙
和⊙ 的半径分别是12和2,圆心
的半径分别是12和2,圆心 是⊙O的直径,
是⊙O的直径, 切⊙O于
切⊙O于 ,
, 交⊙O于
交⊙O于 ,连
,连 .若
.若 ,则
,则 的度数为 .
的度数为 .