Question

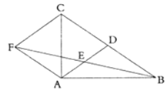
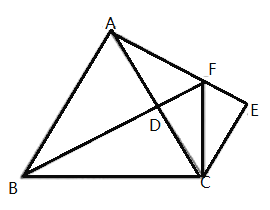
【题目】如图，在等边中，点为上一点，，

（1）求证：≌；

（2）延长交于，连接，若，猜想线段的数量关系，并证明你的猜想．

Answer 1

【答案】（1）见解析；（2），证明见解析

【解析】

（1）由题意利用等边三角形的性质以及全等三角形的判定进行分析求证即可；

（2）根据题意利用垂直平分线定理以及全等三角形性质求得△ABF是含30°角的直角三角形即可分析求证.

解：（1）∵△ABC是等边三角形 ，

∴BC=AC，∠BCD=60°，

∵，，

在△BCD和△ACE中，

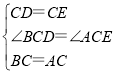
∴△BCD≌△ACE（SAS）.

（2）BF=2AF，

理由：∵AF=CF，AB=BC，

∴BF⊥AC且平分AC（垂直平分线定理），

∴BD为等边△ABC中AC边上的高，

∴BD平分∠ABC，

∴∠ABD=∠DBC=30°，

∵△BCD≌△ACE，

∴∠DBC=∠CAE，

∴∠ABD=∠CAE=30°，

∴∠BAF=∠BAC+∠CAE=90°，

∴在Rt△ABF中，BF=2AF．