��Ŀ����
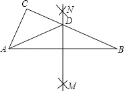
����Ŀ����ͼ������ABC�У�AB��AC����B��40������D���߶�BC���˶���D����B��C�غϣ�������AD������ADE��40����DE���߶�AC�ڵ�E��

��1������BDA��115�������BAD���� ������DEC���� ����
��2����DC��AB����֤����ABD�ա�DCE��
��3���ڵ�D���˶������У���ADE����״�����ǵ����������������ԣ���ֱ��д����BDA�Ķ������������ԣ���˵�����ɣ�
���𰸡���1��25��115����2�������������3������BDA��110���80��ʱ����ADE�ǵ��������Σ�
��������
��1�������������ڽǺͶ���������֪��ֵ���뼴�������BAD������ƽ��Ϊ180���Լ��������ڽǺ�Ϊ180�����������DEC�Ķ�����
��2���������ɵá�EDC����DAB����B����C��DC��AB������ASA����֤�����ۣ�
��3������ADE�ǵ��������Σ���Ϊ����������ٵ�AD��AEʱ����ADE����AED��40�������ݡ�AED����C���ó���ʱ�����ϣ��ڵ�DA��DEʱ�������DAE����DEA��70���������BAC�Ķ��������������ε��ڽǺͶ��������BAD�����������ε��ڽǺͶ��������BDA���ɣ��۵�EA��EDʱ�������DAC�������BAD�Ķ��������������ε��ڽǺͶ��������BDA�Ķ�����
��1���⣺�ߡ�BDA��115������B��40����
���BAD��180������ABD����BDA��180����40����115����25����
��AB��AC����B��40����
���C��40����
�ߡ�BDA+��ADE+��EDC��180������ADE��40������BDA��115����
���EDC��180����115����40����25����
�ߡ�EDC+��C+��DEC��180����
���DEC��180����25����40����115����
�ʴ�Ϊ��25��115��
��2��֤�����ߡ�EDC+��EDA+��ADB��180������DAB+��B+��ADB��180������B����EDA��40����
���EDC����DAB��
�ߡ�B����C��DC��AB��
���ABD�ա�DCE��ASA����
��3���⣺��BDA��80�� ����BDA��110����
��AB��AC��
���B����C��40����
����AD��AEʱ����ADE����AED��40����
�ߡ�AED����C��
����ʱ�����ϣ�
����DA��DEʱ������DAE����DEA��![]() ��180����40������70����
��180����40������70����
�ߡ�BAC��180����40����40����100����
���BAD��100����70����30����
���BDA��180����30����40����110����
����EA��EDʱ����ADE����DAE��40����
���BAD��100����40����60����
���BDA��180����60����40����80����
������BDA��110����80��ʱ����ADE�ǵ��������Σ�