题目内容
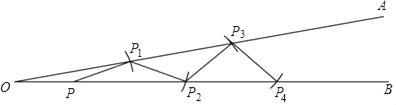
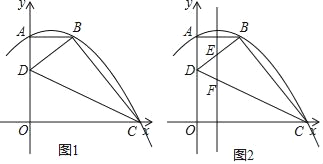
【题目】已知,如图1,O是坐标原点,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,AB⊥y轴于点A,AB=2,AO=4,OC=5,点D是线段AO上一动点,连接CD、BD.
(1)求出抛物线的解析式;
(2)如图2,抛物线的对称轴分别交BD、CD于点E、F,当△DEF为等腰三角形时,求出点D的坐标;
(3)当∠BDC的度数最大时,请直接写出OD的长.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+4;(2)当△DEF为等腰三角形时,点D的坐标为(0,
x+4;(2)当△DEF为等腰三角形时,点D的坐标为(0,![]() )或(0,
)或(0,![]() )或(0,12﹣2
)或(0,12﹣2![]() );(3)
);(3)![]()
【解析】
(1)先确定出点A,B,C的坐标,进而用待定系数法即可得出结论;
(2)先判断出要△DEF是等腰三角形,即:△BDH是等腰三角形,设出点D坐标,进而表示出BD,DH,BH,分三种情况建立方程求解即可得出结论;
(3)先判断出∠BDC最大时,BD⊥BC,进而利用相似三角形建立方程求解即可得出结论.
(1)∵AB⊥y轴于点A,AB=2,AO=4,OC=5,
∴A(0,4),B(2,4),C(5,0),
∵抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,
∴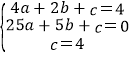 ,
,
∴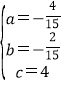 ,
,
∴抛物线解析式为y=-![]() x2-
x2-![]() x+4;
x+4;
(2)如图,
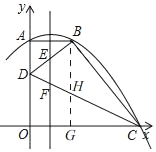
过点B作BG⊥OC于G,交CD于H,
∴点H,G的横坐标为2,
∵EF⊥OC,
∴EF∥BH,
∵△DEF是等腰三角形,
∴△BDH是等腰三角形,
设D(0,5m)(0≤m≤![]() ),
),
∵C(5,0),
∴直线CD的解析式为y=﹣mx+5m,
∴H(2,3m),
∴BH=4﹣3m,
∴BH2=9m2﹣24m+16,DH2=4+(5m﹣3m)2=4+4m2,BD2=4+(5m﹣4)2=25m2﹣40m+20,
当BD=DH时,25m2﹣40m+20=4+4m2,
∴m=![]() (舍)或m=
(舍)或m=![]() ,
,
∴5m=![]() ,
,
∴D(0,![]() ),
),
当BD=BH时,25m2﹣40m+20=9m2﹣24m+16,
∴m=![]() ,
,
∴D(0,![]() ),
),
当BH=DH时,9m2﹣24m+16=4+4m2,
∴m=![]() 或m=
或m=![]() (舍去),
(舍去),
∴D(0,12﹣2![]() ),
),
即:当△DEF为等腰三角形时,点D的坐标为(0,![]() )或(0,
)或(0,![]() )或(0,12﹣2
)或(0,12﹣2![]() );
);
(3)如图1,
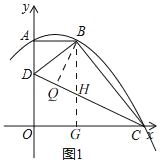
过点B作BG⊥OC于G,交CD于H,
∴四边形OABG是矩形,点H,G的横坐标为2,
∴∠OAB=∠ABG=90°,
∴OG=2,
∵OC=5,
∴CG=3,
∵B(2,4),
∴BG=4,
过点B作BQ⊥CD,
∴∠BQD=90°,
∴要∠BDC最大,
∴∠DBQ最小,
即:BD⊥BC时,∠DBQ最小,
∴∠DBC=90°=∠ABG,
∴∠ABD=∠CBG,
∵∠BGC=∠BAD=90°,
∴△ABD∽△GBC,
∴![]() ,
,
∴![]() ,
,
∴AD=![]() ,
,
∴OD﹣OA﹣AD=![]() .
.

 阅读快车系列答案
阅读快车系列答案