题目内容
【题目】如图,在 Rt△ABC 中,∠C=90°,AC=8cm,BC=6cm,M 在 AC上,且AM=6cm,过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC,若动点 P 从点 A 出发,沿射线 AN 匀速运动,运动速度为 1cm/s,设点 P 运动时间为 t 秒.
(1)经过 秒时,Rt△AMP 是等腰直角三角形?
(2)经过几秒时,PM⊥MB?
(3)经过几秒时,PM⊥AB?
(4)当△BMP 是等腰三角形时,直接写出 t 的所有值.

【答案】(1)6;(2)2;(3)8;(4)2或![]() .
.
【解析】
(1)得出腰时AM=AP,即可得出答案;
(2)根据垂直的定义和同角的余角相等得到∠CBM=∠AMP,证明△CBM≌△AMP,根据全等三角形的性质得到 AP=CM=2,根据题意得到答案;
(3)证明△APM≌△CAB,根据全等三角形的性质得到 AP=CA=8,根据题意得到答案;
(4)分 MB=MP 和 PB=PM 两种情况,根据全等三角形的性质,勾股定理计算即可.
(1)当 Rt△AMP 是等腰直角三角形时,AP=AM=6cm,
∴t=6÷1=6(s),
故答案为:6;
(2)当 PM⊥MB 时,∠BMP=90°,
∴∠BMC+∠AMP=90°,又∠BMC+∠CBM=90°,
∴∠CBM=∠AMP,
在△CBM 和△AMP 中,
 ,
,
∴△CBM≌△AMP(ASA),
∴AP=CM=2,
∴t=2,即经过 2 秒时,PM⊥MB;
(3)当 PM⊥AB 时,如图1,∠PHA=90°,
∴∠HPA+∠HAP=90°,又∠HAP+∠CAB=90°,
∴∠APM=∠CAB,
在△APM 和△CAB 中,
 ,
,
∴△APM≌△CAB(ASA),
∴AP=CA=8,
∴t=8,
∴经过 8 秒时,PM⊥AB;

(4)根据勾股定理得,BM=![]() ,BP 的最小值为 8,
,BP 的最小值为 8,
∵![]() <8,
<8,
∴BM≠BP,
当 MB=MP 时,
在 Rt△BCM 和 Rt△MAP 中,
![]() ,
,
∴Rt△BCM≌Rt△MAP(HL),
∴AP=CM=2, 则 t=2,
当 PB=PM 时,如图2,作BF⊥AN于 F, 则四边形 BCAF 为矩形,
∴BF=CA=8,AF=BC=6,
∴PF=6﹣t,
由勾股定理得,BP2=PF2+BF2,MP2=AM2+AP2,
∴PF2+BF2=AM2+AP2,即(6﹣t)2+82=62+t2, 解得,t=![]() ,
,
∴当△BMP 是等腰三角形时,t=2 或![]() .
.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
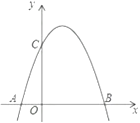
暑假作业安徽少年儿童出版社系列答案【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y= ![]() 的图象上,OA=1,OC=6,则正方形ADEF的边长为 .
的图象上,OA=1,OC=6,则正方形ADEF的边长为 . 
【题目】为了“让所有的孩子都能上得起来,都能上好学”,国家自2007年起出台了一系列“资助贫困学生”的政策,其中包括向经济困难的学生免费提供教科书的政策.为确保这项工作顺利实施,学校需要调查学生的家庭情况.以下是某市城郊一所中学甲、乙两个班的调查结果,整理成表(一)和图(一):
| 城镇户口 (非低保) | 农村户口 | 城镇低保 | 总人数 |
甲班/人 | 20 | 5 |
| |
乙班/人 | 28 | 22 | 4 |
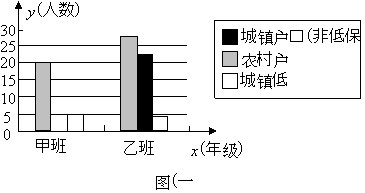
(1)将表(一)和图(一)中的空缺部分补全;
(2)现要预定2009年下学期的教科书,全额100元.若农村户口学生可全免,城镇低保的学生可减免![]() 城镇户口(非低保)学生全额交费.求乙班应交书费多少元?甲班受到国家资助教科书的学生占全班人数的百分比是多少?
城镇户口(非低保)学生全额交费.求乙班应交书费多少元?甲班受到国家资助教科书的学生占全班人数的百分比是多少?
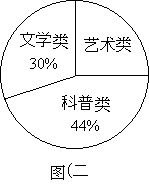
(3)五四青年节时,校团委免费赠送给甲、乙两班若干册科普类、文学类及艺术类三种图书,其中文学类图书有15册,三种图书所占比例如图(二)所示,求艺术类图书共有多少册?
【题目】某大型超市投入15000元资金购进![]() 、
、![]() 两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
类别/单价 | 成本价(元/箱) | 销售价(元/箱) |
A品牌 | 20 | 32 |
B品牌 | 35 | 50 |
(1)该大型超市购进![]() 、
、![]() 品牌矿泉水各多少箱?
品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?