Question

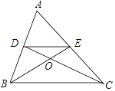
【题目】如图，在△ABC中，两条中线BE、CD相交于点O，则S△ADE：S△COE=________．

Answer 1

【答案】3：2

【解析】

由题意可得DE为三角形的中位线，利用中位线定理得到DE与BC平行，可得出三角形ADE与三角形ABC相似，进而得到面积之比，且得到三角形COE与三角形BOC相似，进而求出所求．

∵在△ABC中，两条中线BE、CD相交于点O，

∴DE为中位线，

∴DE∥BC，DE=BC，

∴△ADE∽△ABC，△DOE∽△COB，

∴S△ADE：S△ABC=1：4，S△DOE：S△COB=1：4，

∵OD：OC=1：2，

∴S△DOE：S△COE=1：2，S△DOB：S△COB=1：2，

∴S△COE=S四边形DBCE=×S△ABC=S△ABC，

则S△ADE：S△COE=：=3：2．

故答案为：3：2