题目内容
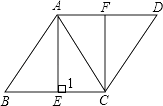
【题目】如图,已知菱形ABCD,AB=AC,E,F分别是BC、AD的中点,连接AE、CF. 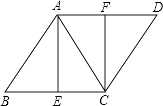
(1)证明:四边形AECF是矩形;
(2)若AB=8,求菱形的面积.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AB=BC,
又∵AB=AC,
∴△ABC是等边三角形,
∵E是BC的中点,
∴AE⊥BC(等腰三角形三线合一),
∴∠1=90°,
∵E、F分别是BC、AD的中点,
∴AF= ![]() AD,EC=
AD,EC= ![]() BC,
BC,
∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∴AF∥EC且AF=EC,
∴四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形),
又∵∠1=90°,
∴四边形AECF是矩形(有一个角是直角的平行四边形是矩形);
(2)解:在Rt△ABE中,AE= ![]() =4
=4 ![]() ,
,
所以,S菱形ABCD=8×4 ![]() =32
=32 ![]() .
.
【解析】(1)根据菱形的四条边都相等可得AB=BC,然后判断出△ABC是等边三角形,然后根据等腰三角形三线合一的性质可得AE⊥BC,∠AEC=90°,再根据菱形的对边平行且相等以及中点的定义求出AF与EC平行且相等,从而判定出四边形AECF是平行四边形,再根据有一个角是直角的平行四边形是矩形即可得证;(2)根据勾股定理求出AE的长度,然后利用菱形的面积等于底乘以高计算即可得解.
【考点精析】本题主要考查了勾股定理的概念和菱形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度/厘米 | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少?