��Ŀ����
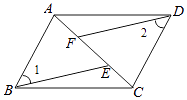
����Ŀ����ͼ1����A������Ϊ��0��3��������A����ƽ��6����λ�õ���B������B��BC��x����C��
��1����B��C�������꼰�ı���AOCB�������
��2����Q��O����1����λ/����ٶ���y���������˶�����P��C����2����λ/����ٶ���x���������˶������˶�ʱ��Ϊt�루0��t��3�����Ƿ����һ��ʱ�䣬ʹ��S��BOQ�� ![]() �������ڣ����t��ȡֵ��Χ���������ڣ�˵�����ɣ�
�������ڣ����t��ȡֵ��Χ���������ڣ�˵�����ɣ�
��3����֤��S�ı���BPOQ��һ����ֵ��
���𰸡�
��1���⣺�ߵ�A������Ϊ��0��3��������A����ƽ��6����λ�õ���B������B��BC��x����C��
��B��6��3����C��6��0����
S�ı���AOCB=3��6=18��
��2���⣺����t��ֵʹS��BOQ�� ![]() S��BOP��
S��BOP��
�������£�
��S��BOQ= ![]() ��6t=3t��
��6t=3t��
S��BOP= ![]() ��3��6��2t��=9��3t��
��3��6��2t��=9��3t��
��3t�� ![]() ��9��3t��
��9��3t��
��ã�t��1��
��0��t��1ʱ��S��BOQ�� ![]() S��BOP��
S��BOP��
��3��֤������S�ı���BPOQ=S�ı���AOCB��S��AQB��S��BCP
=18�� ![]() ��3��t����6��
��3��t����6�� ![]() ��3��2t
��3��2t
=3t+��9��3t��
=9��
��S�ı���BPOQ��һ����ֵ��
��������Ҫ�ѹ�������������IJ���ʽת��Ϊ����ʱ��t�IJ���ʽ�������������������ѧ�Ļ����������ı��������ֵ�������ͨ�����㻯���һ����ʱ��t�صij���.

 ��ʦ�㾦�ִʾ��ƪϵ�д�
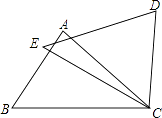
��ʦ�㾦�ִʾ��ƪϵ�д�����Ŀ����֪��A��B��C�����ɡ�ABC����ƽ�Ƶõ��ģ����Ǹ�������ƽ��ֱ������ϵ�е��������±���ʾ��
��ABC | A��a��0�� | B��3��0�� | C��5��5�� |
��A��B��C�� | A�䣨4��2�� | B�䣨7��b�� | C�䣨c��7�� |
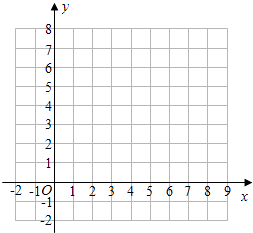
��1���۲���и���Ӧ������ı仯������գ�a= �� b= �� c=��
��2����ƽ��ֱ������ϵ�л�����ABC��ƽ�ƺ�ġ�A��B��C�䣻
��3��ֱ��д����A��B��C�������� ��