题目内容
如图，已知平行四边形ABCD中，F、G是AB边上的两个点，且FC平分∠BCD，GD平分∠ADC，FC与GD相交于点E，求证：AF=GB．
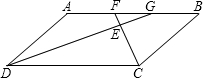
证明：在平行四边形ABCD中，
∵DG、CF分别平分∠ADC、∠BCD，
∴∠ADG=∠CDG，∠DCF=∠BCF，
又∵∠CDG=∠AGD，∠DCF=∠BFC，
∴∠ADG=∠AGD，∠BCF=∠BFC，
∴AG=AD，BF=BC，
又∵AD=BC，
∴AG=BF，
∴AF=GB．
∵DG、CF分别平分∠ADC、∠BCD，
∴∠ADG=∠CDG，∠DCF=∠BCF，
又∵∠CDG=∠AGD，∠DCF=∠BFC，
∴∠ADG=∠AGD，∠BCF=∠BFC，
∴AG=AD，BF=BC，
又∵AD=BC，
∴AG=BF，
∴AF=GB．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
相关题目
