题目内容
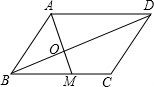
如图，已知?ABCD中，点M是BC的中点，且AM=6，BD=12，AD=4
，则该平行四边形的面积为（ ）
| 5 |
A．24
| B．36 | C．48 | D．72 |
AM、BD相交于点O，
在平行四边形ABCD中，可得△BOM∽△AOD，
∵点M是BC的中点，即
=
，、
∴
=
=
，
∵AM=6，BD=12，
∴OM=2，OB=4，
在△BOM中，22+42=(2
)2，
∴OB⊥OM
∴S△ABD=
BD•OA
=
×12×4=24，
∴SABCD=2S△ABD=48．
故选C．
在平行四边形ABCD中，可得△BOM∽△AOD，
∵点M是BC的中点，即
| BM |
| AD |
| 1 |
| 2 |
∴
| OB |
| OD |
| OM |
| OA |
| 1 |
| 2 |
∵AM=6，BD=12，
∴OM=2，OB=4，
在△BOM中，22+42=(2
| 5 |
∴OB⊥OM
∴S△ABD=
| 1 |
| 2 |
=
| 1 |
| 2 |
∴SABCD=2S△ABD=48．
故选C．
练习册系列答案
阅读快车系列答案
相关题目
