Question

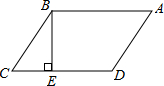
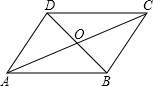
如图，在?ABCD中，AB=5，AD=10，cosB=

3

5

，过BC的中点E作EF⊥AB，垂足为点F，连接DF，求DF的长．

Answer 1

延长DC，FE相交于点H．
∵四边形ABCD是平行四边形，
∴AB∥DC，AB=CD，AD=BC，
∴∠B=∠ECH，∠BFE=∠H．
∵AB=5，AD=10，
∴BC=10，CD=5．
∵E是BC的中点，
∴BE=EC=

1

2

BC=5．
在△BFE和△CHE中，

∠BFE=∠H ∠BEF=∠CEH BE=CE

，
∴△BFE≌△CHE（AAS），
∴CH=BF，EF=EH．
∵EF⊥AB，
∴∠BFE=∠H=90°．
在Rt△BFE中，
∵cosB=

BF

BE

=

3

5

，
∴BF=CH=3．
∴EF=

BE2-BF2

=4，DH=8．
在Rt△FHD中，∠H=90°，
∴DF²=FH²+DH²=8²+8²=2×8²．
∴DF=8

2

．