题目内容
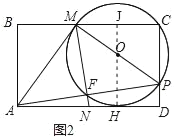
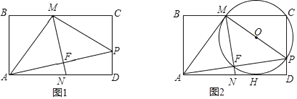
【题目】如图所示，将矩形纸片ABCD折叠，使得顶点A与边CD上的动点P重合（点P不与点C、D重合），MN为折痕，点M、N分别在边BC、AD上，连结AM、MP、AP，其中，AP与MN相交于点F．⊙O过点M、C、P
（1）若∠AMP＝90°，求证：BM＝CP；
（2）随着点P的运动，若⊙O与AM相切于点M，又与AD相切于点H，且AB＝4，求CP的长．
【答案】（1）证明见解析；（2）3.
【解析】
(1)由矩形的性质得出∠B=∠C=90°,证出∠BAM=∠CMP,由折叠的性质得出AM=PM,由AAS证明△ABM≌△MPC，即可得出结论；
(2)连接HO并延长交BC于J,根据折叠的性质知：MN垂直平分AP,可得：AM=PM,AM为⊙O的切线,可得：∠AMP=∠CMP+∠AMB=90°,又∠BAM+∠AMB=90°,可得：∠CMP=∠BAM,∠B=∠C=90°,可证：△ABM≌△MCP,MC=AB,BM=CP,由AD为⊙O的切线,可得：OJ⊥AD,故：JH∥CP,△MOJ∽△MPC,设PD的长为x,则PC=ABx,OJ=
PC，OH=ABOJ可求出⊙O的半径，在Rt△MCP中，运用勾股定理可将PD的长求出，即可得出CP的长.
（1）证明：∵四边形ABCD是矩形，
∴∠B＝∠C＝90°，
∴∠BAM+∠AMB＝90°，
∵∠AMP＝90°，
∴∠AMB+∠CMP＝90°，
∴∠BAM＝∠CMP，
由折叠的性质得：MN垂直平分AP，
∴AM＝PM，
在△ABM和△MPC中，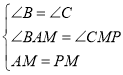
，
∴△ABM≌△MPC（AAS），
∴BM＝CP；
（2）解：∵AM是⊙O的切线，
∴∠AMP＝90°，
∴∠CMP+∠AMB＝90°，
∵∠BAM+∠AMB＝90°，
∴∠CMP＝∠BAM，
由折叠的性质得：MN垂直平分AP，
∴MA＝MP，
∵∠B＝∠C＝90°，
∴△ABM≌△MCP，
∴MC＝AB＝4
设PD＝x，则CP＝4﹣x，
∴BM＝PC＝4﹣x，
连接HO并延长交BC于J，如图2所示：
∵AD是⊙O的切线，
∴∠JHD＝90°，
∴HDCJ为矩形，
∴OJ∥CP，
∴△MOJ∽△MPC，
∴OJ：CP＝MO：MP＝1：2，
∴OJ＝（4﹣x），
OH＝MP＝4﹣OJ＝（4+x），
∵MC2＝MP2﹣CP2，
∴（4+x）2﹣（4﹣x）2＝16，
解得：x＝1，即PD＝1，
∴PC＝3．
