题目内容
【题目】如图,![]() 和
和![]() 都是等边三角形,连接AC,DE,CD.
都是等边三角形,连接AC,DE,CD.
(1)猜想AC与DE的数量关系,并说明理由。
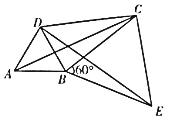
(2)给出定义:若一个四边形中存在一组邻边的平方等于一条对角线的平方,则这个四边形为勾股四边形.如图,若![]() ,求证:四边形ABCD是勾股四边形。
,求证:四边形ABCD是勾股四边形。
(3)设![]() ,
,![]() ,
,![]() 的面积分别是
的面积分别是![]() ,若
,若![]() ,试探究
,试探究![]() 与
与![]() 之间满足的等量关系。
之间满足的等量关系。
【答案】(1) AC=DE,理由见解析;(2)见解析;(3)![]()
【解析】
(1)证明△ABC≌△DBE即可得AC=DE;
(2)先证明△CDE为直角三角形, 得CE+CD=DE,再由CE=CB,DE=AC得CB+CD=AC,从而得出结论;
(3) 分别表示出S,S, S,再结合线段找出它们之间的关系.
(1)解: ∵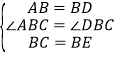 ,
,
∴△ABC≌△DBE(ASA),
∴AC=DE;
(2)证明: ∵∠DCE=90°,
∴△CDE为直角三角形,
∴CE+CD=DE,
又∵CE=CB,DE=AC,
∴CB+CD=AC,
∴四边形ABCD是勾股四边形;
(3)解:在等边△ABD与等边△BCE中,
S=![]() BD ,S=
BD ,S=![]() BC;
BC;
在直角三角形DBC中,S=![]() BD·BC,
BD·BC,
∵S·S=![]() (BD·BC) =
(BD·BC) =![]() (
(![]() (BD·BC) =
(BD·BC) =![]() S ,
S ,
∴![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目