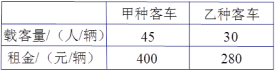题目内容
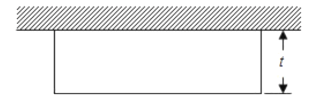
【题目】有长为l的篱笆,利用它和房屋的一面墙围成如图形状的园子,园子的宽为t.
(1)用关于l,t的代数式表示园子的面积;这个代数式是多项式还是单项式?
(2)若l=100固定不变,若t的值取20,25,30时,则哪一种取法所围成的园子面积最大?
【答案】(1)面积为tl-2t2; 是多项式.(2)当t取25时围成的园子面积最大
【解析】
(1)因为篱笆的长为l,当宽为t时,根据图形可知园子的长为l﹣2t,那么根据长方形的面积公式可知面积为t(l﹣2t);观察即可得出是多项式
(2)分别求出t的值取20,25,30时,园子面积,比较面积即可.
解:(1)由题意可知:篱笆的长为l,当宽为t时,园子的长为l﹣2t,则面积为t(l﹣2t)=![]() ,可知这个式子是多项式;
,可知这个式子是多项式;
(2)l=100,当t=20时,t(l﹣2t)=20×(100﹣2×20)=1200;
l=100,当t=25时,t(l﹣2t)=25×(100﹣2×25)=1250;
l=100,当t=30时,t(l﹣2t)=30×(100﹣2×30)=1200;
∴当t取25时围成的园子面积最大.

【题目】综合与实践
元且期间,我市各大商场掀起购物狂湖,现有甲、乙、丙三个商场开展的促销活动如表所示:
商场 | 优惠活动 |
甲 | 全场按标价的 |
乙 | 实行“满 (如:顾客购衣服 |
丙 | 实行“满 |
根据以上活动信息,解决以下问题:
(1)三个 商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场更划算?
(2)黄 先生发现在甲、乙商场同时出售一件标价![]() 元的上衣和一条标价
元的上衣和一条标价![]() 多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
多元的裤子,最后付款也一样,诸问这条裤子的标价是多少元?
(3)丙商场又推出 “先打折”,“再满![]() 减
减![]() 元”的活动,张先生买了一件标价为
元”的活动,张先生买了一件标价为![]() 元的上衣,张先生发现竟然比没打折前多付了
元的上衣,张先生发现竟然比没打折前多付了![]() 元钱,问丙商场先打了多少折后再参加活动?
元钱,问丙商场先打了多少折后再参加活动?