��Ŀ����
����Ŀ����֪������y��x2+��1��2a��x��2a��a�dz�������
��1��֤��������������x�����н��㣻
��2�������������x���һ������ΪA��m��0������2��m��5����a��ȡֵ��Χ��
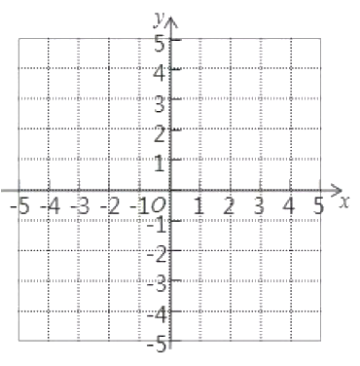
��3���ڣ�2���������£���aΪ����������������x���·��IJ�����x�����Ϸ��ۣ����ಿ�ֱ��ֲ��䣬�õ�һ����ͼ��G����������ͼ��̽��ֱ��y��kx+1��kΪ����������ͼ��G����������������
���𰸡���1������������2��1��a��![]() ����3����ͼ��G��������2����
����3����ͼ��G��������2����
��������
��1���������ߵ�yֵ����0��֤���÷��̵ġ���0���ɣ�
��2������A����������m��ֵ��������a��ȡֵ��Χ��
��3����k��0��k��0����������ۣ����ͼ�����⣮
�⣺��1����y��0����0��x2+��1��2a��x��2a��
�ߡ�����1��2a��2��4��1������2a������1+2a��2��0��
��x2+��1��2a��x��2a��0��ʵ������
�����������x�����н��㣻
��2������������x���һ������ΪA��m��0����
��0��m2+��1��2a��m��2a��
��m����1��m��2a��
��2��m��5��
��2��2a��5��
��1��a��![]() ��
��
��3����1��a��![]() ����a������
����a������
��a��2��
�������߽���ʽΪ��y��x2��3x��4��
��ͼ����k��0ʱ��
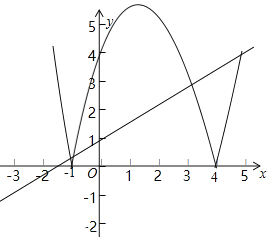
��y��kx+1���㣨��1��0��ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������3����
��k��1��
��0��k��1ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������4����
��k��1ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������2����
��ͼ����k��0ʱ��
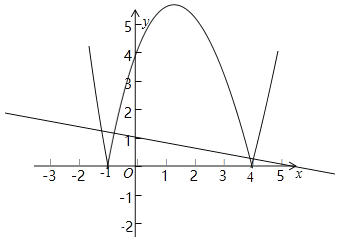
��y��kx+1���㣨4��0��ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������3����
��k����![]() ��
��
����![]() ��k��0ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������4����
��k��0ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������4����
��k����![]() ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������2����
ʱ��ֱ��y��kx+1��kΪ����������ͼ��G��������2����

 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�