Question

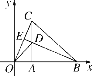
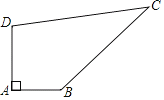
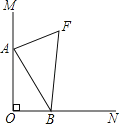
【题目】如图，∠MON＝90°，OB＝4，点A是直线OM上的一个动点，连结AB，作∠MAB与∠ABN的角平分线AF与BF，两条角平分线所在的直线相交于点F，则点A在运动过程中线段BF的最小值为（　　）

A. 4B. C. 8D. 2

Answer 1

【答案】D

【解析】

分情况讨论：当点A在射线OM上时，过F作FE⊥ON于E，FH⊥OM于H，FG⊥AB于G，由角平分线的性质得出FH＝FG，FG＝FE，得出FH＝FE，证出点F在∠MON的角平分线上；当点A在射线OM的反向延长线上时，同理得出点F在∠MON的角平分线上；当BF⊥OF时，BF取最小值，证出△BOF是等腰直角三角形，即可得出答案．

解：当点A在射线OM上时，过F作FE⊥ON于E，FH⊥OM于H，FG⊥AB于G，

如图1所示：

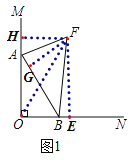
∵AF与BF分别是∠MAB与∠ABN的角平分线，

∴FH＝FG，FG＝FE，

∴FH＝FE，

∴点F在∠MON的角平分线上；

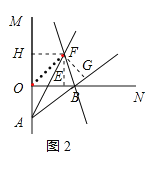
当点A在射线OM的反向延长线上时，过F作FE⊥ON于E，FH⊥OM于H，FG⊥AB交AB的延长线于G，

如图2所示：

∵AF与BF分别是∠MAB与∠ABN的角平分线，

∴FH＝FG，FG＝FE，

∴FH＝FE，

∴点F在∠MON的角平分线上；

综上所述，点F在∠MON的角平分线上，

∴当BF⊥OF时，BF取最小值，

∵∠MON＝90°，OB＝4，

∴∠FON＝∠MON＝45°，

∴△BOF是等腰直角三角形，

∴BF＝OB＝2；

故选：D．