题目内容
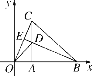
【题目】如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=![]() ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
【答案】(1,![]() -1)或(-
-1)或(-![]() ,
,![]() )
)
【解析】
试题∵OB=CB,OB边上的高CA与OC边上的高BE相交于点D,AB=![]() ,∠CBO=45°,∴AB=AC=
,∠CBO=45°,∴AB=AC=![]() ,OD=CD,在Rt△BAC中,BC=
,OD=CD,在Rt△BAC中,BC=![]() =2,∴OB=2,∴OA=OB﹣AB=
=2,∴OB=2,∴OA=OB﹣AB=![]() ,在Rt△OAC中,OC=
,在Rt△OAC中,OC=![]() =
=![]() ,在Rt△OAD中,
,在Rt△OAD中,![]() ,
,![]() ,解得AD=
,解得AD=![]() ,∴OD=CD=
,∴OD=CD=![]() ,在Rt△BAD中,BD=
,在Rt△BAD中,BD=![]() =
=![]() ,①如图1,△BMC∽△CDO时,过M点作MF⊥AB于F,
,①如图1,△BMC∽△CDO时,过M点作MF⊥AB于F,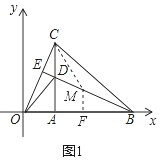
![]() ,即
,即![]() ,解得BM=
,解得BM=![]() ,∵MF⊥AB,CA是OB边上的高,∴MF∥DA,∴△BMF∽△BDA,∴
,∵MF⊥AB,CA是OB边上的高,∴MF∥DA,∴△BMF∽△BDA,∴![]() ,即
,即![]() ,解得BF=1,MF=
,解得BF=1,MF=![]() ,∴OF=OB﹣BF=1,∴点M的坐标是(1,
,∴OF=OB﹣BF=1,∴点M的坐标是(1,![]() );
);
②如图2,△BCM∽△CDO时,过M点作MF⊥AB于F,
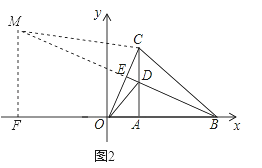
![]() ,即
,即![]() ,解得BM=
,解得BM=![]() ,∵MF⊥AB,CA是OB边上的高,∴MF∥DA,∴△BMF∽△BDA,∴
,∵MF⊥AB,CA是OB边上的高,∴MF∥DA,∴△BMF∽△BDA,∴![]() ,即
,即![]() ,解得BF=
,解得BF=![]() ,MF=
,MF=![]() ,∴OF=BF﹣OB=
,∴OF=BF﹣OB=![]() ,∴点M的坐标是(
,∴点M的坐标是(![]() ,
,![]() ).
).
综上所述,点M的坐标是(1,![]() )或(
)或(![]() ,
,![]() ).
).
故答案为:(1,![]() )或(
)或(![]() ,
,![]() ).
).

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目