题目内容
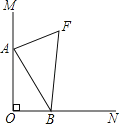
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,A点坐标为(-10,0),对角线AC和OB相交于点D且AC·OB=160.若反比例函数y=![]() (x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
(x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
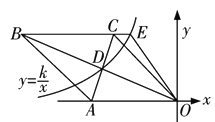
【答案】1:5
【解析】作CG⊥AO,BH⊥AO,根据菱形和三角形的面积公式可得S△OAC=![]() S菱形=40,从而得OA=10,CG=8,在Rt△OGE中,根据勾股定理得OG=6,AG=4,即C(-6,8),根据全等三角形的性质和中点坐标公式可得B(-16,8),D(-8,4),将D代入反比例函数解析式可得k,
S菱形=40,从而得OA=10,CG=8,在Rt△OGE中,根据勾股定理得OG=6,AG=4,即C(-6,8),根据全等三角形的性质和中点坐标公式可得B(-16,8),D(-8,4),将D代入反比例函数解析式可得k,
设E(a,8),将点E坐标代入反比例函数解析式,可得E(-4,8);根据三角形面积公式分别求得S△OCE和S△OAB , 从而得S△OCE:S△OAB.
作CG⊥AO,BH⊥AO,
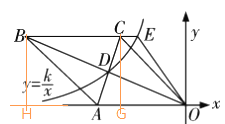
∵BO·AC=160,
∴S菱形=![]() ·BO·AC=80,
·BO·AC=80,
∴S△OAC=![]() S菱形=40,
S菱形=40,
∴![]() ·AO·CG=40,
·AO·CG=40,
∵A(-10,0),
∴OA=10,
∴CG=8,
在Rt△OGE中,
∴OG=6,AG=4,
∴C(-6,8),
∵△BAH≌△COG,
∴BH=CG=8,AH=OG=6,
∴B(-16,8),
∵D为BO的中点,
∴D(-8,4),
又∵D在反比例函数上,
∴k=-8×4=-32,
∵C(-6,8),
∴E(a,8),
又∵E在反比例函数上,
∴8a=-32,
∴a=-4,
∴E(-4,8),
∴CE=2,
∴S△OCE=![]() ·CE·CG=
·CE·CG=![]() ×2×8=8,
×2×8=8,
S△OAB=![]() ·OA·BH=
·OA·BH=![]() ×10×8=40,
×10×8=40,
∴S△OCE:S△OAB=8:40=1:5.
故答案为:1:5.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
增减产值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知该厂星期五生产自行车__________辆.
(2)根据记录的数据可知该厂本周实际生产自行车_________辆.
(3)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元,若没有完成任务,少生产一辆扣20元,那么该厂工人这一周的工作总额是多少元?
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
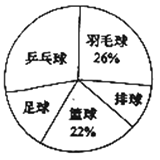
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.