Question

【题目】对于平面直角坐标系xOy中的点P和⊙C，给出如下定义：若⊙C上存在两个点A，B，使得点P在射线BC上，且∠APB＝∠ACB（0°＜∠ACB＜180°），则称P为⊙C的依附点．

（1）当⊙O的半径为1时

①已知点D（﹣1，0），E（0，﹣2），F（2.5，0），在点D，E，F中，⊙O的依附点是　 　；

②点T在直线y＝﹣x上，若T为⊙O的依附点，求点T的横坐标t的取值范围；

（2）⊙C的圆心在x轴上，半径为1，直线y＝﹣2x+2与x轴、y轴分别交于点M、N，若线段MN上的所有点都是⊙C的依附点，请求出圆心C的横坐标n的取值范围．

Answer 1

【答案】（1）①E、F；②＜t＜或﹣＜t＜﹣；（2）2＜n＜或﹣2＜n＜1﹣．

【解析】

（1）①根据P为⊙C的依附点，由圆内角度的相互转换，判断出当r<OP<3r（r为⊙C的半径）时，P为⊙C的依附点，由此即可判断；

②分两种情形：点T在第二象限或第四象限分别求解即可；

（2）分两种情形：点C在点M的右侧，点C在点M的左侧，根据题意分析计算即可．

解：（1）①当⊙O的半径为1时，即圆心C与原点重合，

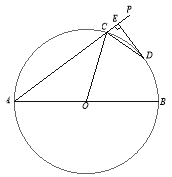
如图，设B、D为圆O与x轴的左右交点，A为圆上任意一点，

∵OA=OD，

∴∠OAD＝∠ODA，

∴∠ADB＝∠AOB，

∵∠APB＝∠AOB，

∴∠ADB＝∠APB，

∴∠DAP＝∠APB，

∴AD＝DP，

当点A和点B重合时，OP＝3r，

当点A与点D重合时，OP＝r，

∵0°＜∠ACB＜180°，即0°＜∠AOB＜180°

∴r＜OP＜3r

根据P为⊙C的依附点，可知：当r＜OP＜3r（r为⊙C的半径）时，点P为⊙C的依附点．

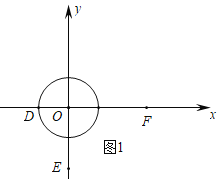
如图1中，∵D(1，0)，E(0，2)，F(2.5，0)，

∴OD＝1，OE＝2，OF＝2.5，

∴1＜OE＜3，1＜OF＜3，

∴点E，F是⊙C的依附点，

故答案为：E、F；

②如图2，

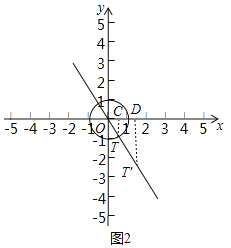
∵点T在直线y=上，

∴点T在第二象限或第四象限，直线y=与x轴所夹的锐角为60°，

当点T在第四象限，当OT＝1时，作CT⊥x轴，易求点，当OT'＝3时，作DT'⊥x轴，易求D，

∴满足条件的点T的横坐标t的取值范围，

当点T在第二象限，同理可得满足条件的点T的横坐标t的取值范围，

综上所述：满足条件的点T的横坐标t的取值范围：或，

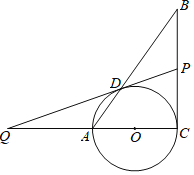
（2）如图3中，当点C在点M的右侧时，

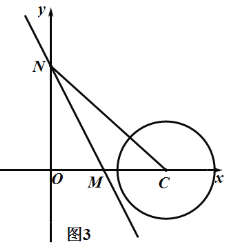
由题意M(1，0)，N(0，2)，

当CN=3时，OC=，此时C，

当CM＝1时，此时C(2，0)，

∴满足条件的n的值的范围为；

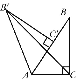
如图4中，当点C在点M的右侧时，

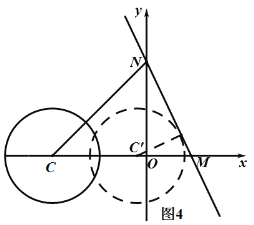
当⊙C与直线MN相切时，

由题意M(1，0)，N(0，2)，∴MN＝，

∴sin∠OMN=，

∴，

∴，

∴，

当CM=3时，C(2，0)，此时，满足题意，

∴满足条件的m的值的范围为，

综上所述，满足条件的n的值的范围为：或．