题目内容
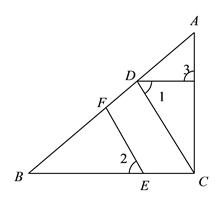
【题目】如图1,在等腰Rt△ABC中,∠ACB=90°,点F是AB上一点,作等腰Rt△FCP,且∠PCF=90°,连结AP.
(1)求证:△CFB≌△CPA;
(2)求证:AP2+AF2=PF2;
(3)如图2,在AF上取点E,使∠ECF=45°,求证:AE2+BF2=EF2.

【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)由△ABC和△PCF都是等腰直角三角形,易得AC=BC,PC=FC,∠ACP=∠BCF可得结论;
(2) 由(1)可得∠PAC=∠B=45°,可得∠PAF=∠PAC+∠BAC=45°+45°=90°,AP2+AF2=PF2;
(3)连结PE,可证得△PCE≌△FCE(SAS),可得EF=EP,∠PCE=∠ECF=45°,由(2)知可得∠PAF=90°,PA=BF,AP2+AE2=PE2,AE2+BF2=EF2.
解:
(1)证明:∵△ABC和△PCF都是等腰直角三角形,
∴AC=BC,PC=FC,∠ACB=PCF=90°,
∴∠ACB-∠ACF=∠PCF-∠ACF,
∴∠ACP=∠BCF,
在△CFB与△CPA中
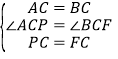
∴△CFB≌△CPA(SAS)
(2)证明:∵△ABC是等腰直角三角形,
∴∠B=∠BAC=45°,
由(1)△CFB≌△CPA,∴∠PAC=∠B=45°,
∴∠PAF=∠PAC+∠BAC=45°+45°=90°,
∴AP2+AF2=PF2
(3)证明:连结PE,
∵∠ACE+∠BCF=∠ACB-∠ECF=90°-45°=45°,
∵∠BCF=∠ACP,
∴∠PCE=∠PCA+∠ACE=45°,
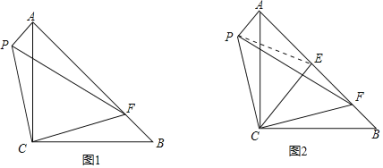
在△PCE与△FCE中
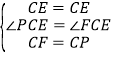
∴△PCE≌△FCE(SAS),
∴EF=EP,∠PCE=∠ECF=45°
由(2)知∴∠PAF=90°,PA=BF,
∴AP2+AE2=PE2;
∴AE2+BF2=EF2 .