题目内容
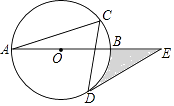
【题目】如图,AB是半圆O的直径,射线AM⊥AB,点P在AM上,连接OP交半圆O于点D,PC切半圆O于点C,连接BC,OC. 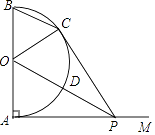
(1)求证:△OAP≌△OCP;
(2)若半圆O的半径等于2,填空: ①当AP=时,四边形OAPC是正方形;
②当AP=时,四边形BODC是菱形.
【答案】
(1)证明:∵PC切半圆O于点C,
∴OC⊥PC,
∵AM⊥AB,
∴∠OAP=90°,
在Rt△OAP和Rt△OCP中
![]() ,
,
∴Rt△OAP≌Rt△OCP
(2)2;2 ![]()
【解析】(2)解:①∵Rt△OAP≌Rt△OCP,
∴PA=PC,
而OA=OC,
∴当AO=AP时,四边形OAPC为菱形,
而∠OAP=90°,
∴四边形OAPC是正方形,
此时AP=OA=2;
②∵四边形BODC是菱形,
∴OB=OD=CD=BC,BC∥OD,
∴△OBC为等边三角形,
∴∠B=60°,
∴∠AOP=60°,
在Rt△OAP中,∵tan∠AOP= ![]() ,
,
∴AP=2tan60°=2 ![]() ,
,
即AP=2 ![]() 时,四边形BODC是菱形.
时,四边形BODC是菱形.
所以答案是2,2 ![]() .
.


练习册系列答案
相关题目