题目内容
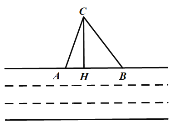
【题目】笔直的河流一侧有一旅游地C,河边有两个漂流点A.B.其中AB=AC,由于某种原因，由C到A的路现在已经不通，为方便游客决定在河边新建一个漂流点H(A，H，B在一条直线上)，并新修一条路CH测得BC=5千米，CH=4干米，BH=3千米，
(1)问CH是否为从旅游地C到河的最近的路线?请通过计算加以说明；
(2)求原来路线AC的长.
【答案】（1）CH是从旅游地C到河的最近的路线，见解析；（2）
千米
【解析】
（1）根据勾股定理的逆定理解答即可；
（2）根据勾股定理解答即可．
解：（1）是，
理由是：在△CHB中，
∵CH2+BH2=（2.4）2+（1.8）2= BC2=25
∴CH⊥AB，
所以CH是从村庄C到河边的最近路.
（2）设AC=x
在Rt△ACH中，由已知得AC=x，AH=x-3，CH=4
由勾股定理得：AC2=AH2+CH2
∴x2=（x-3）2+42
解这个方程，得x=，
答：原来的路线AC的长为千米．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
