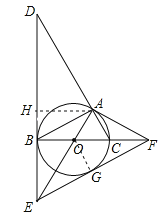
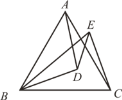【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC= ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.

【答案】(1) 见解析; (2)3 ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)根据圆周角定理得到∠BAC=90°,根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°,∠DBC=90°,于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论;
(2)根据S△AOC= ,得到S△ACF=
,得到S△ACF= ,通过△ACF∽△DAE,求得S△DAE=
,通过△ACF∽△DAE,求得S△DAE= ,过A作AH⊥DE于H,解直角三角形得到AH=
,过A作AH⊥DE于H,解直角三角形得到AH= DH=
DH= DE,由三角形的面积公式列方程即可得到结论;
DE,由三角形的面积公式列方程即可得到结论;
(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG= (180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
(180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
试题解析:(1)证明:∵BC是⊙O的直径,∴∠BAC=90°,∵∠ABC=30°,∴∠ACB=60°
∵OA=OC,∴∠AOC=60°,∵AF是⊙O的切线,∴∠OAF=90°,∴∠AFC=30°,∵DE是⊙O的切线,∴∠DBC=90°,∴∠D=∠AFC=30,∵∠DAE=ACF=120°,∴△ACF∽△DAE;
(2)∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°,∴∠CAF=30°,∴∠CAF=∠AFC,∴AC=CF,∴OC=CF,∵S△AOC= ,∴S△ACF=
,∴S△ACF= ,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=
,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB= BD,∴AF=
BD,∴AF= BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴
BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴ ,∵△ACF∽△DAE,∴
,∵△ACF∽△DAE,∴ =
= ,∴S△DAE=
,∴S△DAE= ,过A作AH⊥DE于H,∴AH=
,过A作AH⊥DE于H,∴AH= DH=
DH= DE,∴S△ADE=
DE,∴S△ADE= DEAH=
DEAH= ×
×
 =
= ,∴DE=
,∴DE=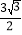 ;
;
(3)∵∠EOF=∠AOB=120°,∴∠OEB=∠AFO,在△AOF与△BOE中,∵∠OBE=∠OAF,∠OEB=∠AFO,OA=OB,∴△AOF≌△BEO,∴OE=OF,∴∠OFG= (180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
(180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
【题型】解答题
【结束】
25
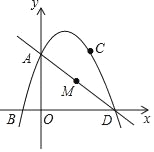
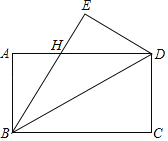
【题目】如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2 ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
(1)填空:点B的坐标为 ;
(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;
(3)①求证: ;
;
②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.

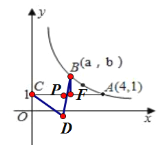
![]() (x>0,k为常数)的图象经过A(4,1),点B(a,b)(0<a<4)是双曲线上的一动点,过A作AC⊥y轴于C,点D是坐标系中的另一点.若以A.B.C.D为顶点的平行四边形的面积为12,那么对角线长度的最大值为_____.
(x>0,k为常数)的图象经过A(4,1),点B(a,b)(0<a<4)是双曲线上的一动点,过A作AC⊥y轴于C,点D是坐标系中的另一点.若以A.B.C.D为顶点的平行四边形的面积为12,那么对角线长度的最大值为_____.
![]()
![]()
![]() 得x=1,则B(1,4)
得x=1,则B(1,4)![]() =
=![]() +
+![]() =10,
=10,![]() ,BD=2BP=2
,BD=2BP=2![]() >AC=4,
>AC=4,![]() >AB=
>AB=![]() .
.![]() >BC=
>BC=![]()
![]() >2
>2![]() >
>![]() .
.![]() .
.
 每课必练系列答案
每课必练系列答案