��Ŀ����
����Ŀ������̽��
![]() ����ͼ
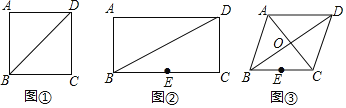
����ͼ![]() ��������ABCD�ĶԽ���BD����һ��P��ʹ
��������ABCD�ĶԽ���BD����һ��P��ʹ![]() ��С��
����
![]() ��ͼ
��ͼ![]() ����PΪ����ABCD�ĶԽ���BD��һ���㣬
����PΪ����ABCD�ĶԽ���BD��һ���㣬![]() ��
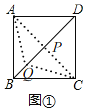
��![]() ����EΪBC�ߵ��е㣬����һ��P��ʹ
����EΪBC�ߵ��е㣬����һ��P��ʹ![]() ��С�����������Сֵ��
��С�����������Сֵ��
������
![]() ��ͼ
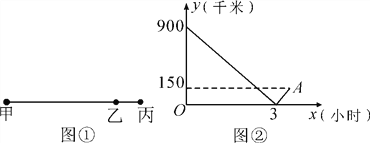
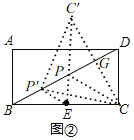
��ͼ![]() ����ʦ����һ��߳�Ϊ1000�����β�ժABCD��
����ʦ����һ��߳�Ϊ1000�����β�ժABCD��![]() �ף�BDΪС·��BC���е�EΪһˮ�أ���ʦ����������С·BD�Ͻ�һ���ο���ʱ��Ϣ������P��Ϊ�˽�ʡ���أ�ʹ��Ϣ������P��ˮ��E�����C�ľ���֮����̣���ô�Ƿ���ڷ��������ĵ�P�������ڣ���������P��λ�ã�����������̾��룻�������ڣ���˵�����ɣ�
�ף�BDΪС·��BC���е�EΪһˮ�أ���ʦ����������С·BD�Ͻ�һ���ο���ʱ��Ϣ������P��Ϊ�˽�ʡ���أ�ʹ��Ϣ������P��ˮ��E�����C�ľ���֮����̣���ô�Ƿ���ڷ��������ĵ�P�������ڣ���������P��λ�ã�����������̾��룻�������ڣ���˵�����ɣ�
���𰸡��⣺![]() ������
������![]()
![]() ����СֵΪ3��
����СֵΪ3��![]() ���ڣ�����̾���ԼΪ985��
���ڣ�����̾���ԼΪ985��
��������
��1����������֮���߶���̣����ɵó����ۣ�
��2����ȷ������P��λ�ã��������CBD=30�㣬�����жϳ���BCC'�ǵȱ������Σ����ɵó����ۣ�
��3����ȷ������P��λ�ã������OA��OB����������������AH������ù��ɶ������ɵó����ۣ�
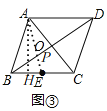
�⣺![]() ��ͼ
��ͼ![]() ������AC��BD�ڵ�P�����P������Ҫ�����ĵ㣬
������AC��BD�ڵ�P�����P������Ҫ�����ĵ㣬
���ɣ���BD����ȡһ�����ڵ�P�ĵ�Q������AQ��CQ��
![]() ��
��
![]() ��ͼ
��ͼ![]()
 ��
��
����C����BD�ĶԳƵ�C'������EC'��BD�ڵ�P������C'P��
�ߵ�C���C'����BD�ĶԳƵ㣬
��CP=C'P��
��C'P+PE=C'P'+P'E=C'E��
��BD����ȡ���ڵ�P��P'������P'E��P'C��C'P'��
��C'P'+P'E=P'C+P'E��C'E��
���P������Ҫ�����ĵ㣬EC'�ij���PE+PC����Сֵ��
���ı���ABCD�Ǿ��Σ�![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
�ߵ�C�͵�C'����BD�Գƣ�
��CC'��BD��G��
��BD��CC'�Ĵ�ֱƽ���ߣ�����BC'��
���C'BD=��CBD=30�㣬BC'=BC��
���C'BC=60�㣬
���BCC'�ǵȱ������Σ�
�ߵ�E��BC���е㣬
��CE��BC��
![]() ��
��
![]() ��
��
����![]() ����СֵΪ3��
����СֵΪ3��
![]() ���ڣ���ͼ
���ڣ���ͼ![]() ������AE��BD��P����P������Ҫ�����ĵ㣬AE�ij��Ⱦ�����Ϣ������P��ˮ��E�����C�ľ���֮����̵�ֵ��
������AE��BD��P����P������Ҫ�����ĵ㣬AE�ij��Ⱦ�����Ϣ������P��ˮ��E�����C�ľ���֮����̵�ֵ��
 ��
��
![]() �ı���ABCD�����Σ�
�ı���ABCD�����Σ�
![]() ��C����BD�ĶԳƵ�ΪA������AE����BD��P����P������Ҫ�����ĵ㣬
��C����BD�ĶԳƵ�ΪA������AE����BD��P����P������Ҫ�����ĵ㣬
![]() �ף�
�ף�![]() �ף�
�ף�![]() ��Q��
��Q��
![]() �ף�
�ף�![]() �ף�
�ף�
����A��![]() ��H��
��H��
![]() ��
��
![]() �ף�
�ף�
��![]() �У����ݹ��ɶ����ã�
�У����ݹ��ɶ����ã�![]() �ף�
�ף�
![]() �ף�
�ף�
��![]() ��
�У�![]() �ף�
�ף�
�������ڵ�P������̾���ԼΪ985�ף�