Question

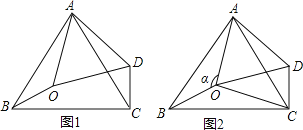
【题目】如图，在四边形ABCD中，∠A=∠C=90°，∠B=α，在AB，BC上分别找一点E,F,使△DEF的周长最小，此时，∠EDF=______。（用含α的代数式表示）

Answer 1

【答案】180°2α

【解析】

根据要使△DEF的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出D关于AB和BC的对称点P,Q,结合四边形的内角和即可得出答案。

如图，作点D关于BA的对称点P，点D关于BC的对称点Q，连接PQ，交AB于E，交BC于F，则点E，F即为所求。

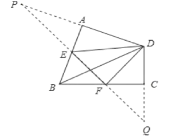
∵四边形ABCD中,∠A=∠C=90°，∠B=α，

∴∠PDQ=180°α，

在三角形PDQ中，∠P+∠Q=180°-∠PDQ =α，

∵点P与点D关于AB对称，点D与点Q关于DQ对称，

∴∠P=∠ADE，∠Q=∠FDQ

∴∠ADE+ FDQ=∠P+∠Q=α

∴∠EDF=∠PDQ-（∠ADE+ ∠FDQ）=180°2α