��Ŀ����
����Ŀ�����������ij��¥�ݹ���10��̨�ף����ijͬѧ����̨��ʱ������һ��1��̨�ף�Ҳ����һ��2��̨�ף���ô��ͬѧ�Ӹö�¥�ݵײ��ϵ��������ж����ֲ�ͬ���߷���
����̽����
Ϊ�������ʵ�����⣬�����Ƚ���������ѧģ�ͣ�
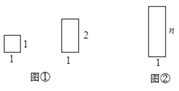
��ͼ�٣������ɸ��߳���Ϊ1�������Σ���Ϊ1��1���Σ������ɸ��߳��ֱ�Ϊ1��2�ľ��Σ���Ϊ1��2���Σ���Ҫƴ��һ����ͼ���б߳��ֱ�Ϊ����n�ľ��Σ���Ϊ1��![]() ���Σ����ж����ֲ�ͬ��ƴ��������
���Σ����ж����ֲ�ͬ��ƴ��������![]() ��ʾ��ͬƴ���ĸ�����
��ʾ��ͬƴ���ĸ�����
Ϊ���������ѧģ�����⣬���Dz�ȡ�IJ��Ժͷ����ǣ�һ���������⻯��
̽��һ���ȴ���������������֣���Ҫƴ��һ��1��1���Σ��ж����ֲ�ͬƴ����
��Ȼ��ֻ��1��ƴ������ͼ�ۣ���![]() =1�֣�
=1�֣�
̽������Ҫƴ��һ��1��2���Σ��ж����ֲ�ͬƴ����
���Կ�������2��ƴ������ͼ�ܣ���![]() =2�֣�
=2�֣�
̽������Ҫƴ��һ��1��3���Σ��ж����ֲ�ͬƴ����
ƴͼ�����ɷ�Ϊ���ࣺһ������ͼ����2��1��2�����Ϸ�����ƴ��һ��1��1���Σ�������ƴ������![]() =2�֣���һ������ͼ���⣱��1��1�����Ϸ�ƴ��һ��1��2���Σ�������ƴ����
=2�֣���һ������ͼ���⣱��1��1�����Ϸ�ƴ��һ��1��2���Σ�������ƴ����![]() =1�֣���ͼ�ݣ���
=1�֣���ͼ�ݣ���![]() =
=![]() +
+![]() = 2+1=3���֣���
= 2+1=3���֣���
![]()
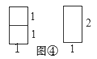
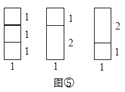
̽���ģ���������̽�����̣�Ҫƴ��һ��1��4���Σ��ж����ֲ�ͬƴ�����뻭ʾ��ͼ˵������������
̽���壺Ҫƴ��һ��1��5���Σ���������̽�����̣��ó�![]() =�������� �ֲ�ͬƴ����
=�������� �ֲ�ͬƴ����
��ֱ��д����������軭ͼ����
��������������������е���ѧģ�ͣ����������������е�ʵ�����⣮
��д�������̣����軭ͼ����
���𰸡�̽���ģ�5; ̽����:8,89
������������ͼ���о�����Ϲ��ɵó�A1��5=A1��3+A1��4��A1��n=A1����n��1��+A1����n��2��������������ɣ�
̽������

ƴͼ�����ɷ�Ϊ������һ������ͼ����2��1��2�����Ϸ�����ƴ��һ��1��2������������ƴ������A1��2 =2������һ������ͼ����3��1��3�����Ϸ�����ƴ��һ��1��1������������ƴ������A1��3 =3��������ͼ����A1��4 =![]() +
+![]() =3+2=5���֣���
=3+2=5���֣���
̽��������A1��4=A1��2+A1��3=5��A1��5=A1��3+A1��4=3+5=8����Ҫƴ��һ��1��5��������8�ֲ�ͬƴ��A1��5��
�ʴ�Ϊ��8��
����������¥�ݹ���10��̨�������ijͬѧ����̨��ʱ������һ��1��̨����Ҳ����һ��2��̨����A1��1=1������A1��3=A1��2+A1��1=2+1=3���֣���A1��4=A1��3+A1��2=3+2=5���֣���A1��5=8���֣�����A1��6=A1��4+A1��5=5+8=13��A1��7=A1��6+A1��5=13+8=21����A1��8=A1��6+A1��7=13+21=34����A1��9=A1��7+A1��8=21+34=55����A1��10=A1��8+A1��9=34+55=89��
������ͬѧ�Ӹö�¥�ݵײ��ϵ���������89�ֲ�ͬ���߷���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�