Question

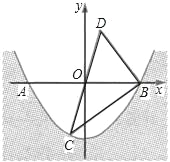
【题目】已知抛物线y＝﹣x2+bx+c经过点C（0，3），与x轴交于A，B两点，点A（﹣1，0）．

（I）求该抛物线的解析式；

（Ⅱ）D为抛物线对称轴上一点，当△ACD的周长最小时，求点D的坐标；

（Ⅲ）在抛物线上是否存在一点P，使CP恰好将以A，B，C，P为顶点的四边形的面积分为相等的两部分？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（I）y＝﹣x2+2x+3；（Ⅱ）点D（1，2）；（Ⅲ）点P（5，﹣12）．

【解析】

（1）抛物线y＝﹣x2+bx+c经过点C（0，3），则抛物线的表达式为：＝﹣x2+bx+3，将点A的坐标代入上式，即可求解；

（2）抛物线的对称轴为：x＝1，点A关于函数对称轴的对称点为点B（3，0），连接BC交抛物线的对称轴于点D，则点D为所求，即可求解；

（3）当点P在第一、二象限时，PC是四边形的边，故CP不可能平分以A，B，C，P为顶点的四边形的面积，当点P在第三、四象限时，设点P（m，﹣m2+2m+3），将点P、C的坐标代入一次函数表达式：y＝sx+n并解得：

直线PC的表达式为：y＝（2﹣m）x+3，过点A、B分别作CP的等距离的平行线m、n，分别交y轴于点M、N，则点C是MN的中点，即6＝3m﹣6+2﹣m，即可求解．

解：（1）抛物线y＝﹣x2+bx+c经过点C（0，3），则抛物线的表达式为：y═﹣x2+bx+3，

将点A的坐标代入上式并解得：b＝2，

故抛物线的表达式为：y＝﹣x2+2x+3；

（2）抛物线的对称轴为：x＝1，点A关于函数对称轴的对称点为点B（3，0），

连接BC交抛物线的对称轴于点D，则点D为所求，

由点B、C的坐标得，直线BC的表达式为：y＝﹣x+3，

当x＝1时，y＝2，

故点D（1，2）；

（3）当点P在第一、二象限时，PC是四边形的边，故CP不可能平分以A，B，C，P为顶点的四边形的面积，

当点P在第三、四象限时，设点P（m，﹣m2+2m+3），

将点P、C的坐标代入一次函数表达式：y＝sx+n并解得：

直线PC的表达式为：y＝（2﹣m）x+3，

过点A、B分别作CP的等距离的平行线m、n，分别交y轴于点M、N，

则直线m的表达式为：y＝（2﹣m）x+k，

将点A的坐标代入上式并解得：k＝3m﹣6，即点M（0，3m﹣6），

同理可得：点N（0，2﹣m），

则点C是MN的中点，即6＝3m﹣6+2﹣m，

解得：m＝5，

故点P（5，﹣12）．