题目内容
如图,正方形ABCD中,BE=CF.
(1)求证:△BCE≌△CDF;
(2)求证:CE⊥DF;
(3)若CD=4,且DG2+GE2=18,则BE= .

(1)求证:△BCE≌△CDF;
(2)求证:CE⊥DF;
(3)若CD=4,且DG2+GE2=18,则BE= .

(1)证明见解析;(2)证明见解析;(3) .
.
 .
.试题分析:(1)根据四边形ABCD是正方形,可得DC=BC,∠DCF=∠CGE,结合BE=CF,于是可以证明△BCE≌△CDF;
(2)由△DCF≌△CBE得到∠BCE=∠CDF,结合角角之间的数量关系,证明出CE⊥DF;
(3)连接DE,首先证明△DGE是直角三角形,利用勾股定理结合正方形的性质即可求出AE.
(1)∵四边形ABCD是正方形,
∴DC=BC,∠DCF=∠CGE,
∵在△DCF和△CBE中,
 ,
,∴△DCF≌△CBE(SAS);
(2)∵△DCF≌△CBE,
∴∠BCE=∠CDF,
∵∠CDF+∠DFC=90°,
∴∠BCE+∠DFC=90°,
∴∠CGF=90°;
(3)连接DE,
∵∠CGF=90°,
∴∠EGD=90°,
∴△DGE是直角三角形,
∵DE2=DG2+GE2=18,
∵CD=4,
∴AD=CD=4,
∴AE=
 .
.
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目



 ≈1.73)
≈1.73) ,
,

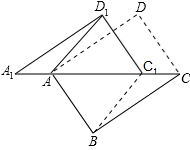
 中,
中, ,
, 是边
是边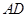 的中点,
的中点, 是边
是边 上任一点(不与点
上任一点(不与点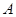 重合)延长
重合)延长 交
交 的延长线于点
的延长线于点 ,连结
,连结 .
. 四边形
四边形 是平行四边形.
是平行四边形. 为何值时,四边形
为何值时,四边形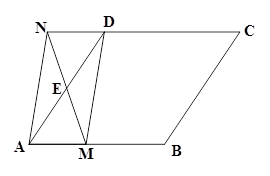


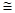 △CC1B;②当x=l时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;④
△CC1B;②当x=l时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;④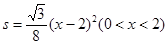 ;其中正确的是 (填序号)
;其中正确的是 (填序号)