题目内容
如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E, AB=2cm.则图中阴影部分面积为 .


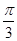 .
.试题分析:根据正方形的性质,可得边相等,角相等,根据扇形BAC与扇形CBD的弧交于点E,可得△BCE的形状,根据图形的割补,可得阴影的面积是扇形,根据扇形的面积公式,可得答案.
正方形ABCD中,
∴∠DCB=90°,DC=AB=2cm.
扇形BAC与扇形CBD的弧交于点E,
∴△BCE是等边三角形,∠ECB=60°,.
∴∠DCE=∠DCB-∠ECB=30°.
根据图形的割补,可得阴影的面积是扇形DCE,
S扇形DCE=×22×
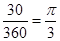 .
.
练习册系列答案
相关题目
 ,四边形ABCF的面积为S
,四边形ABCF的面积为S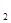 ,请直接写出S
,请直接写出S


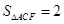 ,那么
,那么 =_____。
=_____。



