Question

【题目】（1）观察下列图形与等式的关系，并填空：

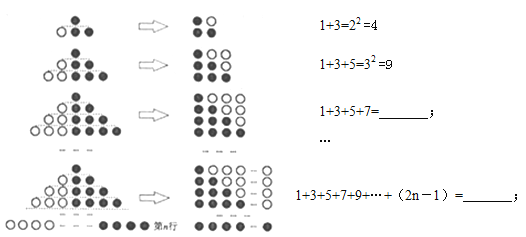
（2）利用（1）中结论，解决下列问题：

①1+3+5+…+203=　 　；

②计算：101+103+105+…+199；

Answer 1

【答案】（1）42=16； n2；（2）①10404； ②7500

【解析】

（1）可以看出连续奇数的和等于数的个数的平方；
（2）①由1+3=4=22，1+3+5=9=32，1+3+5+7=16=42，1+3+5+7+9=25=52，…可以看出连续奇数的和等于数的个数的平方，因此得到一般规律．

②根据1到199的和减去1到99的和即可.

（1）1+3+5+7=16=42=16；1+3+5+7+9….+（2n-1）=n2,

（2）①因为1+3=4=22，

1+3+5=9=32，

1+3+5+7=16=42，

1+3+5+7+9=25=52，

…

1+3+5+7+…+203=1022=10404，

②101+103+105+…+199=（1+3+5+…+199）-（1+3+5+…+99）=1002-502=7500.