��Ŀ����
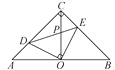
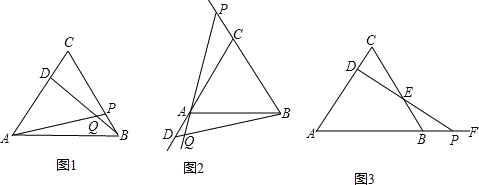
����Ŀ����֪��ͼ����ADC����BDE��Ϊ���������Σ���CAD=��DBE��AC=AD��BD=BE������CE����GΪCE���е㣬����E��AC��ƽ�������߶�AG�ӳ��߽��ڵ�F��
��1����A��D��B������ͬһֱ����ʱ����ͼ1������֤��GΪAF���е㣻
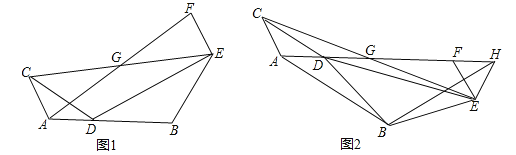
��2����ͼ1����BDE�Ƶ�D��ת��ͼ2λ��ʱ����A��D��G��F��ͬһֱ���ϣ���H���߶�AF���ӳ����ϣ���EF=EH������AB��BH�����ж���ABH����״����˵�����ɣ�

���𰸡���1��֤������������2����ABHΪ���������Σ����ɼ�����.
�������������������1������AC��EF���ɵ���ACG=��FEG�����ݵ�GΪCE���е����ɵ�CG=EG���ٸ�����AGC=��FGE�����ɵó���ACG�ա�FEG�������õ�GΪAF���е���
��2��������ACG�ա�FEG���ɵ�AC=FE���ٸ���AC=AD��FE=HE�����ɵõ�AD=HE�������ı����ڽǺ��Լ�ͬ�ǵIJ�����ȿɵ���BEH=��BDA���ٸ���BD=BE�����ɵõ���ADB�ա�HEB���ɵ�AB=HB������ABH�ǵ��������Σ�
���������������1����AC��EF�����ACG=��FEG���ߵ�GΪCE���е�����CG=EG���֡���AGC=��FGE�����ACG�ա�FEG����AG=FG����GΪAF���е���
��2����ABH��������������������
ͬ��1����֤��ACG�ա�FEG����AC=FE���֡�AC=AD��FE=HE����AD=HE����
��AC��EF�����GFE=��CAD=��DBE����EF=EH�����EFH=��EHF������EFH+��GFE=180�㣬���FHE+��DBE=180�㣬���ı���BDHE������BEH+��BDF=180�����֡���BDA+��BDF=180�㣬���BEH=��BDA����
����BD=BE����
�����٢ڢۣ��ɵ���ADB�ա�HEB����AB=HB������ABH�ǵ��������Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�