题目内容
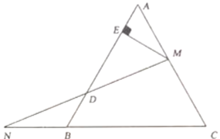
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是中线,过
是中线,过![]() 点作
点作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() .
.
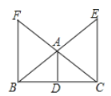
(1)求证:![]() 为等腰三角形;
为等腰三角形;
(2)延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)由等腰三角形的性质得出AD⊥BC,BD=CD,证出CE⊥BC,AD是△BCE的中位线,得出AB=AE,即可得出结论;
(2)由等腰三角形的性质得出∠ABC=∠ACB,∠ABF=∠F,由三角形内角和定理得出2(∠ABF+∠ABC)=180°,得出∠FBC=90°,即可得出BF⊥BC.
(1)证明:∵AB=AC,AD是中线,
∴AD⊥BC,BD=CD,
∵CE∥AD,
∴CE⊥BC,AD是△BCE的中位线,
∴AB=AE,
∵AB=AC,
∴AC=AE,
∴△ACE为等腰三角形;
(2)证明:∵AB=AC,AF=AC,
∴∠ABC=∠ACB,AB=AF,
∴∠ABF=∠F,
∴2(∠ABF+∠ABC)=180°,
∴∠FBC=90°,
∴BF⊥BC.

【题目】我们约定:如果身高在选定标准的±2%范围之内都称为“普启遍身高”.为了了解某校九年级男生中具有“普遍身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
男生 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
身高x(cm) | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
根据以上信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普遍身高”是哪几位男生?并说明理由.
【题目】为了倡导“全民阅读”,某校为调查了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成统计图表如下:
学生家庭藏书情况扇形统计图

类别 | 家庭藏书 | 学生人数 |
|
| 16 |
|
|
|
|
| 50 |
|
| 70 |
根据以上信息,解答下列问题:
(1)共抽样调查了______名学生,![]() ______;
______;
(2)在扇形统计图中,“![]() ”对应扇形的圆心角为_______
”对应扇形的圆心角为_______![]() ;
;
(3)若该校有2000名学生,请估计全校学生中家庭藏书超过60本的人数.