题目内容
【题目】在△ABC中,∠B=90°![]() ∠A
∠A
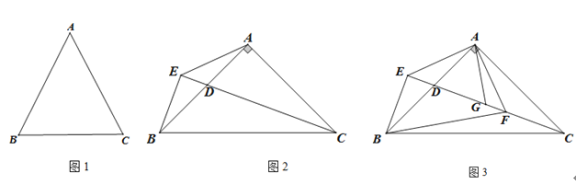
(1)如图1,求证:AB=AC;
(2)如图2,若∠BAC=90°,点D为AB上一点,过点B作直线CD的垂线,垂足为E,连接AE, 求∠AEC的度数;
(3)如图3,在(2)的条件下,过点A作AE的垂线交CE于点F,连接BF,若∠ABF-∠EAB=15°,G为DF上一点,连接AG,若∠AGD=∠EBF,AG=6,求CF的长.
【答案】(1)证明见详解;(2)45°;(3)6
【解析】
(1)利用三角形内角和定理求出![]() ,即可证明
,即可证明![]() ,即可证明AB=AC;
,即可证明AB=AC;
(2)在CE上截取CF=BE,连接AF,通过证明![]() ,可得证明
,可得证明![]() 是等腰直角三角形,从而求出∠AEC;
是等腰直角三角形,从而求出∠AEC;
(3)由(2)![]() 得出
得出![]() ,证明
,证明![]() ,得出
,得出![]() ,利用角的转换求出∠AGD=∠EBF=60°,再根据30°直角三角形的性质求出EF,然后再根据勾股定理求出CF的长度.
,利用角的转换求出∠AGD=∠EBF=60°,再根据30°直角三角形的性质求出EF,然后再根据勾股定理求出CF的长度.
解:(1)![]() =
=![]()
![]()
![]()
=90°![]() ∠A
∠A
∴![]()
∴AB=AC
(2)如图:
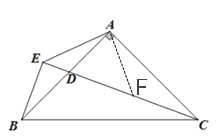
在CE上截取CF=BE,连接AF
由(1)得AB=AC
![]()
∴![]()
又![]() ∠BAC=90°,
∠BAC=90°,![]() (对顶角)
(对顶角)
∴![]()
在![]() 和
和![]() 中
中
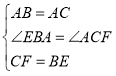
∴![]()
∴AE=AF, ![]()
又![]() ∠BAC=∠DAF+∠FAC=90°
∠BAC=∠DAF+∠FAC=90°
∴∠DAF+∠EAB=90°
∴EAF是等腰直角三角形
∴∠AEC=45°
(3)如图:作AH![]() EC
EC
由(2)得![]()
![]() (对顶角相等)
(对顶角相等)
![]()
![]()
![]()
又![]() ∠ABF-∠EAB=15°
∠ABF-∠EAB=15°
![]()
![]()
![]()
![]()
![]()
∴∠AGD=∠EBF=60°
∴在RtAHG中,HG=![]()
![]()
∴EF=![]()
在RtBEF中 ,设BE=x,则BF=2x
∴![]()
解得:![]()
∴BE=6
∴CF=BE=6

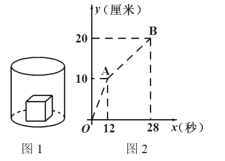
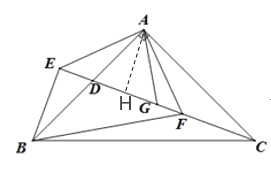
【题目】如图,△ABC中,AB=BC=5cm,AC=6cm,点P从顶点B出发,沿B→C→A以每秒1cm的速度匀速运动到A点,设运动时间为x秒,BP长度为ycm.某学习小组对函数y随自变量x的变化而变化的规律进行了探究.下面是他们的探究过程,请补充完整:
(1)通过取点,画图,测量,得到了x(秒)与y(cm)的几组对应值:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.5 | 4.1 | 4 | 4.5 | 5.0 |
要求:补全表格中相关数值(保留一位小数);
(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
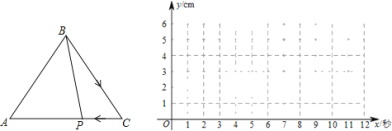
(3)结合画出的函数图象,解决问题:当x约为______时,BP=CP.
【题目】我们约定:如果身高在选定标准的±2%范围之内都称为“普启遍身高”.为了了解某校九年级男生中具有“普遍身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
男生 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
身高x(cm) | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
根据以上信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,找出这10名男生中具有“普遍身高”是哪几位男生?并说明理由.