题目内容
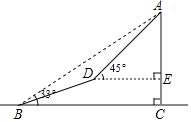
【题目】如图,四边形 ABCD 中,AD∥BC,DC⊥BC,将四边形沿对角线 BD 折叠,点 A 恰好落在 DC 边上的 点 A'处,若∠A'BC=20°,则∠A'BD 的度数为_____.

【答案】25°
【解析】
根据AD∥BC,DC⊥BC,∠A'BC=20°,再利用三角形外角的性质,可求得∠DA'B的度数,由折叠的性质,可得:∠A=∠DA'B=110°,∠ABD=∠A'BD,继而求得∠A'BD的度数.
∵AD∥BC,DC⊥BC
∴∠C=90°
∵∠A'BC=20°
∴∠D A'B=∠A'BC +∠C=20°+90°=110°
由折叠的性质可得:∠A=∠D A'B =110°,∠ABD=∠A'BD
∵AD∥BC
∴∠ABC=180°-∠A=180°-110°=70°
∴∠A'BD=![]()
故填25°.

练习册系列答案
相关题目
【题目】甲、乙两名同学进行了6轮投篮比赛,两人的得分情况统计如下:
第1轮 | 第2轮 | 第3轮 | 第4轮 | 第5轮 | 第6轮 | |
甲 | 10 | 14 | 12 | 18 | 16 | 20 |
乙 | 12 | 11 | 9 | 14 | 22 | 16 |
下列说法不正确的是( )
A. 甲得分的极差小于乙得分的极差 B. 甲得分的中位数大于乙得分的中位数
C. 甲得分的平均数大于乙得分的平均数 D. 乙的成绩比甲的成绩稳定