��Ŀ����
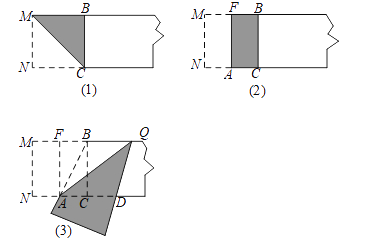
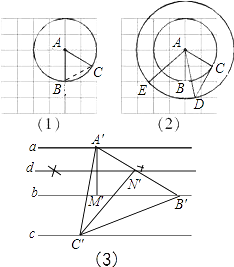
����Ŀ�����������������Ե�AΪԲ�ģ�ABΪ�뾶��ԲA�������ڵ�C����ͼ��1����������C��Բ�����߽������ڵ�D���Ե�AΪԲ�ģ�ADΪ�뾶��Բ�������ڵ�E����ͼ��2������ ���⣺
��1�����ABC�Ķ�����
��2����֤����AEB�ա�ADC��
��3����AEB���Կ������ɡ�ADC���������ı任�õ��ģ����жϡ�AED����״������˵�����ɣ���
��4����ͼ��3������ֱ֪��a��b��c����a��b��b��c����ͼ����ֱ�ߡ����ǰ塢Բ�滭�ȱ�������A��B��C�䣬ʹ��������A�䣬B�䣬C�䣬�ֱ���ֱ��a��b��c�ϣ�Ҫ��д����Ҫ�Ļ�ͼ���̣�����Ҫ˵�����ɣ�
���𰸡�
��1���⣺����BC���������֪��C��AB���д����ϣ�
��AC=BC��
��AB=AC����AB=BC=AC������ABC�ǵȱ������Σ�
���ABC=60�㣻
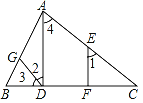
��2���⣺��CD�С�A�ڵ�C��
���ACD=90���ABE=��ACD=90�㣬
��Rt��AEB��Rt��ADC��
��AB=AC��AE=AD��
��Rt��AEB��Rt��ADC��HL��
��3���⣺��AEB���Կ������ɡ�ADC�Ƶ�A˳ʱ����ת60��õ��ģ�
��AED�ǵȱ�������
��4���⣺����ֱ��a����ȡһ�㣬��Ϊ��A�䣬��A��M���b������Ϊ��M�䣻�����߶�A��M��Ĵ�ֱƽ���ߣ���ֱ��Ϊֱ��d�����Ե�A��ΪԲ�ģ�A��M�䳤Ϊ�뾶��Բ����ֱ��d���ڵ�N�䣻�ܹ���N����N��C���A��N�佻ֱ��c�ڵ�C�䣬����A��C�䣻���Ե�A��ΪԲ�ģ�A��C�䳤Ϊ�뾶��Բ����Բ��ֱ��b�ڵ�B�䣻������A��B�䡢B��C�䣬���A��B��C��Ϊ����ȱ�������
����������1������BC��ͨ��֤����ABC�ǵȱ������Σ����������ABC�Ķ�������2����Rt��AEB��Rt��ADC�У�ͨ��HL֤����AEB�ա�ADC����3������ת�����ʼ��ɵó���AED�ǵȱ������Σ���4������HL������֤��A��N��C��ա�A��M��B�䣬�á�C��A��N��=��B��A��M�䣬���ǡ�B��A��C��=��M��A��N��=60�㣬��A��B��=A��C��á�A��B��C��Ϊ�ȱ������Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�