题目内容
【题目】下面我们做一次折叠活动:
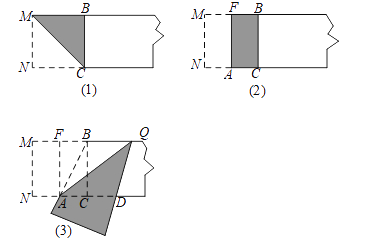
第一步,在一张宽为2的矩形纸片的一端,利用图(1)的方法折出一个正方形,然后把纸片展平,折痕为MC;
第二步,如图(2),把这个正方形折成两个相等的矩形,再把纸片展平,折痕为FA;
第三步,折出内侧矩形FACB的对角线AB,并将AB折到图(3)中所示的AD处,折痕为AQ.
根据以上的操作过程,完成下列问题:
(1)求CD的长.
(2)请判断四边形ABQD的形状,并说明你的理由.
【答案】(1)![]() ;(2)四边形ABQD是菱形.
;(2)四边形ABQD是菱形.
【解析】试题分析:(1)首先证明四边形MNCB为正方形,然后再依据折叠的性质得到:CA=1,AB=AD,最后再依据CD=AD-AC求解即可;
(2)根据平行线的性质和折叠的性质可得到∠BAQ=∠BQA,然后依据等角对等边的性质得到AB=BQ,接下来,依据一组对边平行且相等的四边形为平行四边形可证明四边形ABQD是平行四边形,再由AB=AD,可得四边形ABQD是菱形.
试题解析:(1)∵∠M=∠N=∠MBC=90°,
∴四边形MNCB是矩形,
∵MB=MN=2,
∴矩形MNCB是正方形,
∴NC=CB=2,
由折叠得:AN=AC=![]() NC=1,
NC=1,
Rt△ACB中,由勾股定理得:AB=![]() =
=![]() ,
,
∴AD=AB= ![]() ,
,
∴CD=AD﹣AC= ![]() ﹣1;
﹣1;
(2)四边形ABQD是菱形,理由是:
由折叠得:AB=AD,∠BAQ=∠QAD,
∵BQ∥AD,
∴∠BQA=∠QAD,
∴∠BAQ=∠BQA,
∴AB=BQ,
∴BQ=AD,BQ∥AD,
∴四边形ABQD是平行四边形,
∵AB=AD,
∴四边形ABQD是菱形.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目




