题目内容
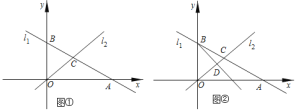
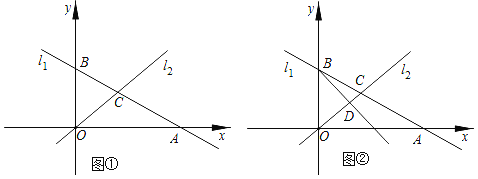
【题目】在平面直角坐标系中，直线l1：y=﹣
x+4分别与x轴、y轴交于点A、点B，且与直线l2：y=x于点C．
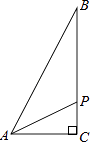
（1）如图①，求出B、C两点的坐标；
（2）若D是线段OC上的点，且△BOD的面积为4，求直线BD的函数解析式．
（3）如图②，在（2）的条件下，设P是射线BD上的点，在平面内是否存在点Q，使以O、B、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．
【答案】（1）C（
，）．（2）y=-x+4．（3）Q的坐标为（2
，-2）或（-2，2）或（4，4）．
【解析】
（1）利用待定系数法求出点B坐标，利用方程组求出点C坐标即可；
（2）设D（m，m），构建方程求出m即可解决问题，再利用待定系数法求出直线的解析式；
（3）分三种情形分别求解即可解决问题；
（1）对于直线：y=-
x+4，令x=0，得到y=4，
∴B（0，4），
由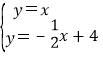
，解得
，
∴C（，）．
（2）∵点D在直线y=x上，设D（m，m），
∵△BOD的面积为4，
∴解得m=2，
∴D（2，2）．
设直线BD的解析式为y=kx+b，则有 
，
解得
，
∴直线BD的解析式为y=-x+4．
（3）如图②中，
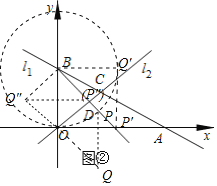
①当OB为菱形的边时，OB=PB=4，可得P（2，4-2），Q（2，-2）．
②当P′B为菱形的对角线时，四边形OBQ′P′是正方形，此时Q（4，4）．
③当OB为菱形的边时，点P″与D重合，P、Q关于y轴对称，Q″（-2，2），
综上所述，满足条件的Q的坐标为（2，-2）或（-2，2）或（4，4）．
【题目】抗震救灾中，某县粮食局为了保证库存粮食的安全，决定将甲、乙两个仓库的粮食，全部转移到具有较强抗震功能的A、B两仓库．已知甲库有粮食100吨，乙库有粮食80吨，而A库的容量为70吨，B库的容量为110吨．从甲、乙两库到A、B两库的路程和运费如下表：（表中“元/吨千米”表示每吨粮食运送1千米所需人民币）
路程（千米） | 运费（元/吨千米） | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
（1）若甲库运往A库粮食x吨，请写出将粮食运往A、B两库的总运费y（元）与x（吨）的函数关系式；
（2）当甲、乙两库各运往A、B两库多少吨粮食时，总运费最省，最省的总运费是多少？
【题目】某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
（1）列函数表达式：若矩形的周长为8，设矩形的一边长为x，面积为y，则有y=____________；
（2）上述函数表达式中，自变量x的取值范围是____________；
（3）列表：
x | … | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y | … | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | … |
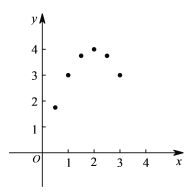
写出m=____________；
（4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象；
（5）结合图象可得，x=____________时，矩形的面积最大；写出该函数的其它性质（一条即可）：____________.
