��Ŀ����
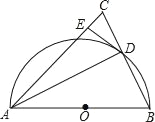
����Ŀ��ij��Ҫ����һ��Բ����ˮ�أ���ˮ�����봹ֱ��ˮ�氲װһ������![]() ����
����![]() ǡ����ˮ�����ģ���װ�����Ӷ���
ǡ����ˮ�����ģ���װ�����Ӷ���![]() ����Բ����ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�
����Բ����ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�![]() ������ƽ���ϣ�ˮ������ĸ߶�
������ƽ���ϣ�ˮ������ĸ߶�![]() ��ˮƽ����
��ˮƽ����![]() ֮��Ĺ�ϵ��ͼ��ʾ������ƽ��ֱ������ϵ���ұ������ߵĹ�ϵʽΪ
֮��Ĺ�ϵ��ͼ��ʾ������ƽ��ֱ������ϵ���ұ������ߵĹ�ϵʽΪ![]() .������������⣺
.������������⣺

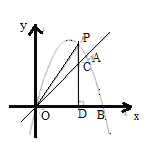
��1����![]() ��Ϊ
��Ϊ![]() ����ʽ����д�������ˮ����ˮƽ������߶��Ƕ����ף�
����ʽ����д�������ˮ����ˮƽ������߶��Ƕ����ף�
��2��д��������������ߵı���ʽ��
��3�������������أ���Ҫʹ�����ˮ�����ڳ��ڣ�ˮ�ص�ֱ������Ҫ�����ף�
���𰸡���1�������ˮ����ˮƽ������߶���4��.��2��![]() .��3��ˮ�ص�ֱ������Ҫ6��.
.��3��ˮ�ص�ֱ������Ҫ6��.
��������
��1�������䷽����һ��ʽת��Ϊ����ʽ��������������ˮ����ˮƽ������߶ȣ�
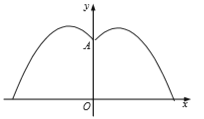
��2�������������ߵĹ���y��Գƣ����������������ߵĶ�����ϵ���Ͷ������꣬�Ӷ������������ߵĽ���ʽ��
��3��������ұ���������x��Ľ���ĺ����꣬���öԳ��Լ������ˮ�ص�ֱ������Сֵ.
�⣺��1����![]() ��
��
�������ߵĶ���ʽΪ![]() .
.
�������ˮ����ˮƽ������߶���4��.
��2�����������ߵĹ���y��Գ�
����������ߵ�a=-1����������Ϊ��-1,4��
��������ߵı���ʽΪ![]() .
.
��3����![]() ����
����![]() ����
����
��![]() ��
��
���![]() ��
��![]() ������������x����ҽ��㣬�ʲ������⣬��ȥ��.
������������x����ҽ��㣬�ʲ������⣬��ȥ��.
��![]() ���ף�
���ף�
��ˮ�ص�ֱ������Ҫ6��.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д�