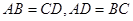题目内容
(8分)如图,梯形ABCD中,AD∥BC,对角线BD的垂直平分线与两底AD、BC分别交于点E、F,判断四边形BEDF的形状并说明理由。

四边形BEDF是菱形
试题分析:解:四边形BEDF是菱形,理由是:∵AD∥BC, ∴∠DEO=∠BFO,∵对角线BD的垂直平分线EF, ∴OB=OD,EF⊥BD,在△EOD和△FOB中∵∠DEO=∠BFO ∠EOD=∠FOB OB=OD,∴△EOD≌△FOB,∴OE=OF,∵OB=OD,∴四边形BEDF是平行四边形,∵EF⊥BD,∴四边形BEDF是菱形。
点评:此种试题,要求学生要全面掌握四边形的证明判定和有关性质,证明较为繁琐,需要学生有耐心,观察力强。

练习册系列答案
相关题目


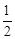 ∠BCA,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠BCA,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
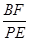 的值;
的值; ,请探究并直接写出
,请探究并直接写出
 cm²
cm²
 cm²
cm² 是平行四边形的是( )
是平行四边形的是( ) ∥
∥ ∥
∥