Question

如图，等腰梯形ABCD中，AD∥BC，AC⊥BD，AD=3，BC=7，试求此等腰梯形的面积．

Answer 1

25

试题分析：过点D作DE∥AC交BC的延长线于E．可证得四边形ACED是平行四边形，即可得到CE=AD=3．DE=AC，从而可得BE=BC+CE=10，再结合等腰三角形的性质可得DE=BD，AC⊥BD，DE∥AC，从而可得DE⊥BD，在Rt△BDE中，根据勾股定理可得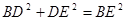，由△ABD和△CDE等底等高可得△ABD和△CDE的面积相等，即可求得结果.
过点D作DE∥AC交BC的延长线于E

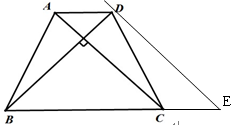
∵等腰梯形ABCD中，AD∥BC
∴四边形ACED是平行四边形
∴CE=AD=3．DE=AC
∴BE=BC+CE=10
又∵等腰梯形ABCD中，AC=BD
∴DE=BD．
∵AC⊥BD，DE∥AC
∴DE⊥BD  
∴在Rt△BDE中，
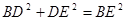
∵BD=DE，BE=10
∴，即
∵△ABD和△CDE等底等高
∴ 
∴
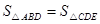
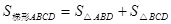
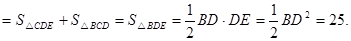
点评：解答本题的关键是读懂题意及图形，正确作出辅助线，把等腰三角形的问题转化为平行四边形和等腰直角三角形的问题.