Question

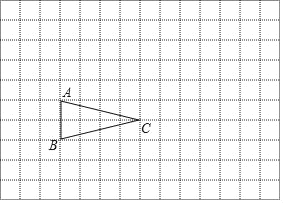
【题目】如图，方格纸中每个小正方形的边长均为1，△ABC的三个顶点均在小正方形的顶点上．

（1）请在方格纸上建立平面直角坐标系，使点A、C的坐标分别为（2，3）、（6，2），并写出点B的坐标；

（2）以原点O为位似中心，在第一象限内将△ABC放大，相似比为2，画出放大后的△A'B'C'；

（3）直接写出B′C′与AC的交点坐标．

Answer 1

【答案】（1）作图见解析；（2）作图见解析；（3）见解析.

【解析】

（1）利用A点和C点坐标画出x轴与y轴，然后写出B点坐标；
（2）把A、B、C三点的横纵坐标都乘以2得到A′、B′、C′的坐标，然后描点即可得到△A′B′C′.（3）根据图象直接得到结论．

解：（1）如图1，B点坐标为（2，1）；

（2）A、B、C的坐标分别为（2，3）、（2，1）（6，2），把A、B、C三点的横纵坐标都乘以2得到A′、B′、C′的坐标，分别为（4，6）、（4，2）、（12，4）然后描点即可得到△A′B′C′.

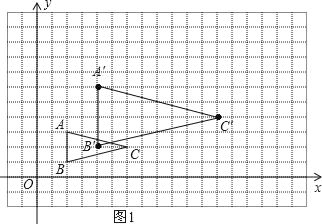
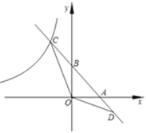
（3）观察图像可知B′C′与AC的交点坐标（5，）．