题目内容
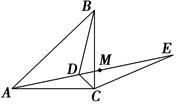
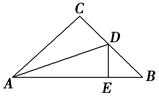
如图,△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAC的外角的平分线,BE⊥AE.

(1)求证:DA⊥AE;
(2)试判断AB与DE是否相等?并证明你的结论.

(1)求证:DA⊥AE;
(2)试判断AB与DE是否相等?并证明你的结论.
见解析
(1)证明:∵∠DAB=
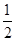 ∠BAC,
∠BAC,∠BAE=
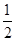 ∠BAF.
∠BAF.∴∠DAB+∠BAE=
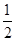 (∠BAC+∠BAF)=
(∠BAC+∠BAF)=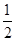 ×180°=90°,即∠DAE=90°,∴DA⊥AE.
×180°=90°,即∠DAE=90°,∴DA⊥AE.(2)解:AB=DE,证明如下;
∵AB=AC,且AD平分∠BAC,∴AD⊥BD,由(1)知AD⊥AE,又∵BE⊥AE,∴四边形ADBE是矩形,∴AB=DE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
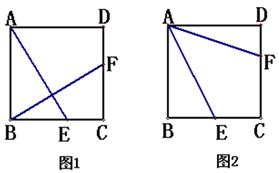
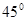 , AE的长为
, AE的长为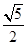 ,试求AF的长度。
,试求AF的长度。