题目内容
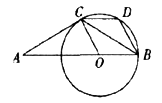
如图,AB是⊙O的直径,点E是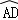 上的一点,∠DBC=∠BED.
上的一点,∠DBC=∠BED.
(1)求证:BC是⊙O的切线;
(2)已知AD=3,CD=2,求BC的长.
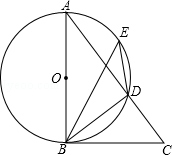
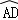 上的一点,∠DBC=∠BED.
上的一点,∠DBC=∠BED.(1)求证:BC是⊙O的切线;
(2)已知AD=3,CD=2,求BC的长.

(1)证明见解析
(2)BC=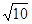
(2)BC=
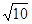
试题分析:(1)由直径所对的圆周角是直角可得∠ADB=90°,从而可得∠BAD+∠ABD=90°,由圆周角定理可得∠BAD=∠DEC及已知可得∠ABC=90°,即BC是⊙O的切线;
(2)由已知可得△ABC∽△BDC,利用对应边成比例即可求出BC的长.
试题解析:(1)∵AB是⊙O的切直径,
∴∠ADB=90°,
又∵∠BAD=∠BED,∠BED=∠DBC,
∴∠BAD=∠DBC,
∴∠BAD+∠ABD=∠DBC+ABD=90°,
∴∠ABC=90°,
∴BC是⊙O的切线;
(2)∵∠BAD=∠DBC,∠C=∠C,
∴△ABC∽△BDC,
∴
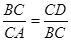 ,即BC2=AC•CD=(AD+CD)•CD=10,
,即BC2=AC•CD=(AD+CD)•CD=10,∴BC=
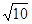 .
.
练习册系列答案
相关题目
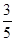 ,OA=10cm,则AB长为 cm.
,OA=10cm,则AB长为 cm.