��Ŀ����
����ѧ��ͨ��ʵ�鷢�֣�����ѧ��������ע������ʱ��仯�����ο�ʼʱ��ѧ��ע��������ǿ���м���һ��ƽ��״̬�����ʼ��ɢ��ѧ��ע����ָ����y��ʱ���t�����ӣ��仯�ĺ���ͼ�����£���0��t��10ʱ��ͼ���������ߵ�һ���֣���10��t��20ʱ��20��t��40ʱ��ͼ�����߶Ρ�
��1����0��t��10ʱ����ע����ָ����y��ʱ��t�ĺ�����ϵʽ��
��2��һ����ѧ̽������Ҫ����24���ӣ�����ʦ�ܷ�ǡ�����ţ�ʹѧ����̽�������ʱ��ע����ָ����������45����ͨ������˵����
��1��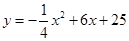 ����2���ܣ����ɼ�������
����2���ܣ����ɼ�������
���������������1��ֱ�����ô���ϵ��������κ�������ʽ�����ó��𰸣�
��2���������ô���ϵ�������һ�κ�������ʽ��������y=45����45=-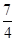 x+95�����x��ֵ�������ó����κ�ע����������45��ʱ�䣮
x+95�����x��ֵ�������ó����κ�ע����������45��ʱ�䣮
��1����0��t��10ʱ���������ߵĺ�����ϵʽΪy=ax2+bx+c����������ͼ���㣨0��25������4��45������10��60����
����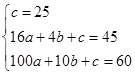 ��
��
��ã�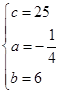 ��
��
����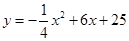 ��
��
��2����20��x��40ʱ���躯������ʽΪ��y=kx+d������20��60������40��25������ã�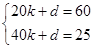 ��
��
��ã�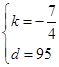
��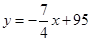 ��
��
��y=45����45=-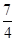 x+95��
x+95��
��ã�x= ��
��
�����κ�� ����ʱע����������45��
����ʱע����������45��
��0��x��10ʱ����y=45����45=- x2+6x+25��
x2+6x+25��
��ã�x1=4��x2=20����ȥ����
�����κ��4����ʱ��ע����������45��
���Խ��κ�ע����������45��ʱ����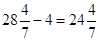 �����ӣ���24�����ӣ���
�����ӣ���24�����ӣ���
������ʦ���Ծ����ʵ��İ��ţ�ʹѧ����̽�������ѧ��ʱ��ע����ָ��������45��
���㣺���κ�����Ӧ�ã�

 ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�ij�̼Ҷ������۾��еط���ɫ��ij����Ʒ��ÿ������Ϊ40Ԫ�������г����飬һ�ܵ�������y�������۵���x��x��50��Ԫ/���Ĺ�ϵ���±���
| ���۵���x ��Ԫ/���� | �� | 55 | 60 | 70 | 75 | �� |
| һ�ܵ�������y ������ | �� | 450 | 400 | 300 | 250 | �� |
��2����һ�ܵ���������ΪSԪ�������S��x�ĺ�����ϵʽ����ȷ�������۵�����ʲô��Χ�ڱ仯ʱ��һ�ܵ����������������۵��۵����������
��3���Ű�����ǣ������������ģ��̼Ҿ�������Ʒһ�ܵ���������ȫ���������������̼ҹ�������Ʒ�Ĵ������10000Ԫ����£�����������̼�����������Ƕ���Ԫ��
 ��������
�������� ����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8.
����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8.
 ��x��0��ͼ����һ�����㣬��PΪԲ�ĵ�Բʼ����y�����У����е�ΪA��
��x��0��ͼ����һ�����㣬��PΪԲ�ĵ�Բʼ����y�����У����е�ΪA�� �������ڣ��������������������M������ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������������������M������ꣻ�������ڣ���˵�����ɣ�
 ����������A��B��D���㣬����D��
����������A��B��D���㣬����D�� ���ƽ���߽��������ڵ�C��ֱ��l����E��0����
���ƽ���߽��������ڵ�C��ֱ��l����E��0����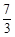 ������ƽ������ABCD�����
������ƽ������ABCD�����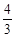 �����P�����꣮
�����P�����꣮
 .����ֱ�ǡ�EFG�У�EF=4�� ��EGF=45��,�ҡ�EFG���ABCDλ��ֱ��AD��ͬ�࣬��F���D�غϣ�GF��AD��ͬһֱ���ϣ���EFG�ӵ�D������ÿ��1����λ���ٶ�������DA����ƽ�ƣ�����G����Aʱֹͣ�˶���ͬʱ��PҲ�ӵ�A��������ÿ��3����λ���ٶ�������AD��DC�����˶��������Cʱֹͣ�˶������˶���ʱ��Ϊt.
.����ֱ�ǡ�EFG�У�EF=4�� ��EGF=45��,�ҡ�EFG���ABCDλ��ֱ��AD��ͬ�࣬��F���D�غϣ�GF��AD��ͬһֱ���ϣ���EFG�ӵ�D������ÿ��1����λ���ٶ�������DA����ƽ�ƣ�����G����Aʱֹͣ�˶���ͬʱ��PҲ�ӵ�A��������ÿ��3����λ���ٶ�������AD��DC�����˶��������Cʱֹͣ�˶������˶���ʱ��Ϊt. �ij��ȣ�
�ij��ȣ� ƽ�ƵĹ����У���
ƽ�ƵĹ����У��� ��ص������Ϊ
��ص������Ϊ ,��ֱ��д�����
,��ֱ��д����� �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д�� ���߶�
���߶�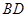 ���ڵ�
���ڵ� ������
������ .�Ƿ����������ʱ��
.�Ƿ����������ʱ�� Ϊ���������Σ������ڣ������Ӧ��
Ϊ���������Σ������ڣ������Ӧ��

 ������t =4��ʱ��
������t =4��ʱ��
